题目内容
已知曲线C1：ρ＝2sinθ，曲线C2：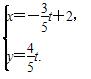
(t为参数)．
(1)化C1为直角坐标方程，化C2为普通方程；
(2)若M为曲线C2与x轴的交点，N为曲线C1上一动点，求|MN|的最大值．
[解析] (1)曲线C1的方程化为ρ2＝2ρsinθ
又x2＋y2＝ρ2，x＝ρcosθ，y＝ρsinθ
所以曲线C1的直角坐标方程x2＋y2－2y＝0，
因为曲线C2的参数方程是
消去参数t得曲线C2的普通方程4x＋3y－8＝0.
(2)在曲线C2的方程中，令y＝0得x＝2，
即M点的坐标为(2,0)，
又曲线C1为圆，其圆心坐标为C1(0,1)，半径r＝1，
则|MC1|＝
，
∴|MN|≤|MC1|＋r＝＋1，|MN|的最大值为＋1.
练习册系列答案
相关题目
＋
＋
＋…＋
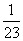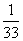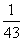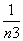，g(n)＝
－
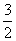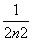，n∈N*.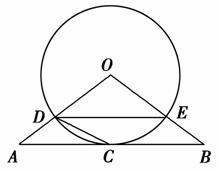
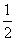，求⊙O的半径r的长．
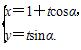(t为参数)，圆C2：ρ＝1.(极坐标轴与x轴非负半轴重合)
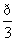时，求直线C1被圆C2所截得的弦长；
.
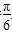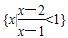，则M∩N等于( )
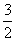} B．{x|
<x<1}
≥
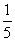|a2－a|对于x∈[2,6]恒成立，则实数a的取值范围是________．