题目内容
在直角坐标系xOy中，已知动点P与平面上两定点M（-1，0），N（1，0）连线的斜率的积为定值-4，设点P的轨迹为C．
（1）求出曲线C的方程；
（2）设直线y=kx+1与C交于A，B两点，若
⊥
，求k的值．
（1）求出曲线C的方程；
（2）设直线y=kx+1与C交于A，B两点，若
| OA |
| OB |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线的定义、性质与方程
分析：（1）根据定点M（-1，0）、N（1，0），直线MP与直线PN的斜率之积为-4，建立方程，化简可得曲线C的方程；
（2）设A（x1，y1），B（x2，y2），联立直线与椭圆方程，利用韦达定理以及
⊥
，推出x1x2+y1y2=0，然后求出直线的斜率的值即可．
（2）设A（x1，y1），B（x2，y2），联立直线与椭圆方程，利用韦达定理以及
| OA |
| OB |
解答：
解：（1）设P点坐标为（x，y）
∵定点M（-1，0）、N（1，0），直线PM与直线PN的斜率之积为-4，
∴
•
=-4，
∴曲线C的方程为x2+
=1(x≠±1)．
（2）设A（x1，y1），B（x2，y2），其坐标满足
消去y并整理得（k2+4）x2+2kx-3=0，
故x1+x2=-
，x1x2=-
．
若
⊥
，即x1x2+y1y2=0．
而y1y2=k2x1x2+k(x1+x2)+1，
于是x1x2+y1y2=-
-
-
+1=0，
化简得-4k2+1=0，所以k=±
．
∵定点M（-1，0）、N（1，0），直线PM与直线PN的斜率之积为-4，
∴
| y |
| x+1 |
| y |
| x-1 |
∴曲线C的方程为x2+
| y2 |
| 4 |
（2）设A（x1，y1），B（x2，y2），其坐标满足
|
消去y并整理得（k2+4）x2+2kx-3=0，
故x1+x2=-
| 2k |
| k2+4 |
| 3 |
| k2+4 |
若
| OA |
| OB |
而y1y2=k2x1x2+k(x1+x2)+1，
于是x1x2+y1y2=-
| 3 |
| k2+4 |
| 3k2 |
| k2+4 |
| 2k2 |
| k2+4 |
化简得-4k2+1=0，所以k=±
| 1 |
| 2 |
点评：本题考查轨迹方程的求解，考查存在性问题的探究，考查直线与椭圆的位置关系，考查转化思想以及计算能力．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知平面向量
，
满足|
|=|
|=2，（
+2
）•（
-
）=-2，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
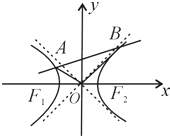如图，F1，F2是双曲线x2-y2=1的两个焦点，O为坐标原点，圆O是以F1F2为直径的圆，直线l：y=kx+b与圆O相切，并与双曲线交于A、B两点．