题目内容
求适合下列条件的圆的方程:
(1)圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2);
(2)过三点A(1,12),B(7,10),C(-9,2).
解 (1)法一 设圆的标准方程为(x-a)2+(y-b)2=r2,
则有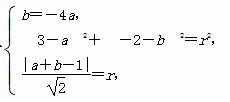
解得a=1,b=-4,r=2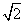 .
.
∴圆的方程为(x-1)2+(y+4)2=8.
法二 过切点且与x+y-1=0垂直的直线为y+2=x-3,与y=-4x联立可求得圆心为(1,-4).
∴半径r=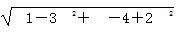 =2
=2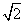 ,
,
∴所求圆的方程为(x-1)2+(y+4)2=8.
(2)法一 设圆的一般方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
则
解得D=-2,E=-4,F=-95.
∴所求圆的方程为x2+y2-2x-4y-95=0.
法二 由A(1,12),B(7,10),
得AB的中点坐标为(4,11),kAB=-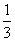 ,
,
则AB的垂直平分线方程为3x-y-1=0.
同理得AC的垂直平分线方程为x+y-3=0.
联立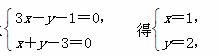
即圆心坐标为(1,2),半径r=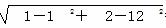 =10.
=10.
∴所求圆的方程为(x-1)2+(y-2)2=100.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
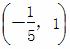 B.
B. 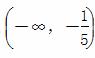 ∪(1,+∞)
∪(1,+∞)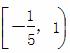 D.
D. 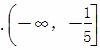 ∪[1,+∞)
∪[1,+∞) (x-1)与圆O:x2+y2=1在第一象限内交于点M,且l与y轴交于点A,则△MOA的面积等于________.
(x-1)与圆O:x2+y2=1在第一象限内交于点M,且l与y轴交于点A,则△MOA的面积等于________.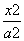 -
-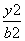 =1(a>0,b>0)的一个焦点与圆x2+y2-10x=0的圆心重合,且双曲线的离心率等于
=1(a>0,b>0)的一个焦点与圆x2+y2-10x=0的圆心重合,且双曲线的离心率等于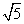 ,则该双曲线的标准方程为( ).
,则该双曲线的标准方程为( ). -
-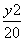 =1 B.
=1 B.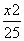 -
-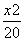 -
-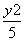 =1 D.
=1 D.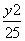 =1
=1