题目内容
15.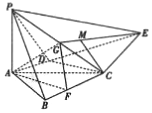 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.(1)求$\frac{ME}{MG}$的值,使得CM∥平面AFG;
(2)求直线CE与平面AFG所成角的正弦值.
分析 (1)推导出∠CAD=60°,∠BAC=60°,由余弦定理得BC=$\sqrt{13}$,从而DE=$\sqrt{13}$,进而得到当$\frac{ME}{MG}=\frac{DE}{DA}=\frac{\sqrt{13}}{2}$时,AG∥DM,平面CDM∥平面AFG,CM∥平面AFG.
(2)分别以DA,AF,AP为x,y,z轴的正方向,建立空间直角坐标系,利用向量法能求出直线CE与平面AFG所成角的正弦值.
解答 解:(1)在Rt△ADC中,∠ADC为直角,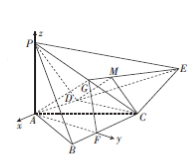
tan$∠CAD=\frac{2\sqrt{3}}{2}=\sqrt{3}$,则∠CAD=60°,
又AC平分∠BAD,∴∠BAC=60°,
∵AB=3,AC=4,∴由余弦定理得BC=$\sqrt{13}$,∴DE=$\sqrt{13}$,
当$\frac{ME}{MG}=\frac{DE}{DA}=\frac{\sqrt{13}}{2}$时,AG∥DM,
又AF∥CD,AF∩AG=A,∴平面CDM∥平面AFG,
∴CM?平面CDM,∴CM∥平面AFG.
(2)分别以DA,AF,AP为x,y,z轴的正方向,建立空间直角坐标系,如图所示,
则A(0,0,0),C(-2,2$\sqrt{3}$,0),D(-2,0,0),G(-1,$\sqrt{3}$,1),E(-2-$\sqrt{13}$,0,0),
$\overrightarrow{AG}$=(-1,$\sqrt{3}$,1),$\overrightarrow{CD}$=(0,-2$\sqrt{3}$,0),$\overrightarrow{CE}$=(-$\sqrt{13}$,-2$\sqrt{3}$,0),
设平面AFG的法向量$\overrightarrow{n}$=(x,y,z),
∵AF∥CD,∴$\overrightarrow{AG}•\overrightarrow{n}$=0,$\overrightarrow{CD}•\overrightarrow{n}$=0,
∴$\left\{\begin{array}{l}{-x+\sqrt{3}y+z=0}\\{-2\sqrt{3}y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
设直线CE与平面AFG所成角为θ,
则sinθ=$\frac{|\overrightarrow{CE}•\overrightarrow{n}|}{|\overrightarrow{CE}|•|\overrightarrow{n}|}$=$\frac{\sqrt{13}}{\sqrt{25}•\sqrt{2}}$=$\frac{\sqrt{26}}{10}$,
∴直线CE与平面AFG所成角的正弦值为$\frac{\sqrt{26}}{10}$.
点评 本题考查满足线面平行的线段比值的求法,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 12$\sqrt{6}$ | B. | 6$\sqrt{6}$ | C. | 12$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
| A. | 3 | B. | $2\sqrt{3}$ | C. | 4 | D. | $3\sqrt{2}$ |
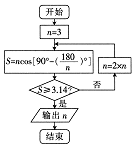 3世纪中期,魏晋时期的数学家刘徽首创“割圆术”,也就是在圆内割正多边形,求的近似值,刘徽容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失唉,当圆内接正多边形的边数无限增加时,多边形面积可无限近圆的面积,利用“割圆术”刘徽得到圆周率精确到小数点后两位的计算值3.14,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:sin15°=0.259)( )
3世纪中期,魏晋时期的数学家刘徽首创“割圆术”,也就是在圆内割正多边形,求的近似值,刘徽容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失唉,当圆内接正多边形的边数无限增加时,多边形面积可无限近圆的面积,利用“割圆术”刘徽得到圆周率精确到小数点后两位的计算值3.14,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:sin15°=0.259)( )