题目内容
4.已知平面向量$\overrightarrow a$,$\overrightarrow b$,$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=2$,且$\overrightarrow a•\overrightarrow b=1$.若$\overrightarrow e$为平面单位向量,$({\overrightarrow a+\overrightarrow b})•\overrightarrow e$的最大值为( )| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{7}$ | D. | 7 |
分析 由已知求出向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角,设出$\overrightarrow{a}=(1,0),\overrightarrow{b}=(1,\sqrt{3})$,再设$\overrightarrow{e}=(cosθ,sinθ)$,然后利用向量的坐标运算求解.
解答 解:由$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=2$,且$\overrightarrow a•\overrightarrow b=1$.
得cos$<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{1×2}=\frac{1}{2}$,
∴$<\overrightarrow{a},\overrightarrow{b}>=60°$,
不妨设$\overrightarrow{a}=(1,0),\overrightarrow{b}=(1,\sqrt{3})$,再设$\overrightarrow{e}=(cosθ,sinθ)$,
∴$({\overrightarrow a+\overrightarrow b})•\overrightarrow e$=(2,$\sqrt{3}$)•(cosθ,sinθ)=$\sqrt{3}sinθ+2cosθ$
=$\sqrt{7}sin(θ+α)$,(tanα=$\frac{2\sqrt{3}}{3}$).
∴$({\overrightarrow a+\overrightarrow b})•\overrightarrow e$的最大值为$\sqrt{7}$.
故选:C.
点评 本题考查平面向量的数量积运算,由题意设出向量的坐标起到事半功倍的效果,是中档题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案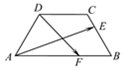 如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )| A. | λ∈($\frac{1}{8}$,$\frac{1}{4}$) | B. | λ∈($\frac{1}{4}$,$\frac{3}{8}$) | C. | λ∈($\frac{3}{8}$,$\frac{1}{2}$) | D. | λ∈($\frac{1}{2}$,$\frac{5}{8}$) |
| A. | (2,3) | B. | (1,3) | C. | (1,2) | D. | (-∞,3) |
| A. | [-2,2) | B. | [1,2) | C. | (-2,1] | D. | (1,2] |
| A. | [-$\frac{2}{3}$,1] | B. | [1,$\frac{3}{2}$] | C. | [$\frac{1}{3}$,$\frac{3}{2}$] | D. | [$\frac{1}{3}$,1] |
| A. | 669 | B. | 670 | C. | 671 | D. | 672 |
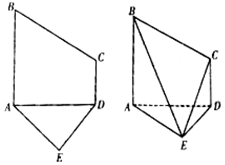 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.