题目内容
7.已知p:$\frac{3}{1-a}$>1,q:?x∈R,ax2+ax-1≥0,r:(a-m)(a-m-1)>0.(1)若p∧q为真,求实数a的取值范围;
(2)若¬p是¬r的必要不充分条件,求m的取值范围.
分析 分别求出p,q,r为真时的a的范围,(1)p∧q为真,则p,q均为真,得到关于a的不等式组,解出即可;
(2)问题转化为r是p的必要不充分条件,得到关于m的不等式,解出即可.
解答 解:(1)p为真时:由$\frac{3}{1-a}$>1解得-2<a<1,
q为真时,当a>0,一定存在ax2+ax-1≥0,当a<0,△=a2+4a≥0,解得a≤-4,
故q为真时,实数a的取值范围为a>0或a≤-4,
∵p∧q为真,则p,q均为真,
∴a的取值范围为(0,1);
(2)关于r:(a-m)(a-m-1)>0,
解得:a>m+1或a<m,
若¬p是¬r的必要不充分条件,
即r是p的必要不充分条件,即p⇒r,
∴m+1≤-2或m>1,即m≤-3或m>1,
故m的取值范围为(-∞,-3]∪(1,+∞).
点评 本题考察了充分必要条件,考察复合命题的判断,考察二次函数的性质,是一道中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
2.已知函数f(x)=a-x+xex,若存在x0>-1,使得f(x0)≤0,则实数a的取值范围为( )
| A. | [0,+∞) | B. | (-∞,0] | C. | [1,+∞) | D. | (-∞,1] |
12.若数列{an}的前n项和Sn=$\frac{2}{3}$an-$\frac{2}{3}$,则数列{an}的通项公式an等于( )
| A. | -2n | B. | (-2)n | C. | -4n | D. | (-4)n |
16.已知函f(x)=$\left\{\begin{array}{l}{2cos\frac{πx}{3}(x≤2000)}\\{{2}^{x-2008}(x>2000)}\end{array}\right.$ 则f[f(2015)]等于( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
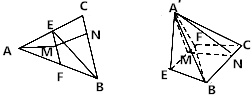 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.