题目内容
1.设函数f(x)=2sin(ωx+ϕ)(-π<ϕ<0),若函数y=f(x)的图象与x轴相邻两个交点间的距离为$\frac{π}{2}$,且图象的一条对称轴是直线x=$\frac{π}{8}$.(1)求ω,ϕ的值;
(2)求函数y=f(x)的单调增区间;
(3)画出函数y=f(x)在区间[0,π]上的图象.
分析 (1)利用正弦函数的图象的周期性求得ω的值,利用正弦函数的图象的对称性求得φ,可得函数的解析式.
(2)利用正弦函数的单调性,求得函数y=f(x)的单调增区间.
(3)利用五点法作图,作出函数y=f(x)在区间[0,π]上的图象.
解答 解:(1)函数y=f(x)的图象与x轴的两个相邻交点间的距离为$\frac{π}{2}$,∴$\frac{1}{2}•\frac{2π}{ω}$=$\frac{π}{2}$,∴ω=2.
又函数图象的一条对称轴是直线$x=\frac{π}{8}$,∴2×$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,k∈Z,
∵-π<ϕ<0,∴φ=-$\frac{3π}{4}$,f(x)=2sin(2x-$\frac{3π}{4}$).
(2)由(1)可知$f(x)=2sin(2x-\frac{3π}{4})$,令2kπ-$\frac{π}{2}$≤2x-$\frac{3π}{4}$≤2kπ+$\frac{π}{2}$ 求得:kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,
可得函数y=f(x)的单调增区间是[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
(3)∵x∈[0,π],则2x-$\frac{3π}{4}$∈[-$\frac{3π}{4}$,$\frac{5π}{4}$],列表:
X | 0 | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | π |
| $2x-\frac{3π}{4}$ | $-\frac{3π}{4}$ | $-\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{5π}{4}$ |
y | $-\frac{{\sqrt{2}}}{2}$ | -2 | 0 | 2 | 0 | $-\frac{{\sqrt{2}}}{2}$ |
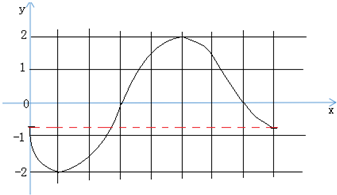 .
.点评 本题主要考查正弦函数的图象和性质,五点法作图,属于中档题.

练习册系列答案
相关题目
16.已知函f(x)=$\left\{\begin{array}{l}{2cos\frac{πx}{3}(x≤2000)}\\{{2}^{x-2008}(x>2000)}\end{array}\right.$ 则f[f(2015)]等于( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
9.已知等差数列{an}中,a3+a7=8,则该数列前9项和S9等于( )
| A. | 4 | B. | 8 | C. | 36 | D. | 72 |
11.若函数y=sinωx在(0,$\frac{π}{2}$)上为增函数,则ω的取值范围是( )
| A. | (-∞,1] | B. | [-1,0) | C. | (0,1] | D. | [1,+∞) |
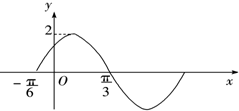 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.