题目内容
10.若实数x、y满足$\left\{\begin{array}{l}{-2x+1≤y≤2x-1}\\{0<x≤3}\end{array}\right.$,则x-2y的取值范围是[-7,13].分析 作出题中不等式组表示的平面区域,得如图的△ABC及其内部,再将目标函数z=x-2y对应的直线进行平移,求出最优解,可得x-2y的取值范围.
解答 解:作出不等式组$\left\{\begin{array}{l}{-2x+1≤y≤2x-1}\\{0<x≤3}\end{array}\right.$,表示的平面区域: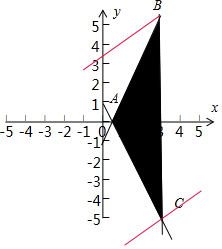
得到如图的△ABC及其内部,其中A($\frac{1}{2}$,0),B(3,5),C(3,-5)
设z=F(x,y)=x-2y,将直线l:z=x-2y进行平移,
当l经过点B时,目标函数z达到最大值,得z最大值=F(3,-5)=13;
当l经过点A时,目标函数z达到最小值,得z最小值=F(3,5)=-7
因此,x+2y的取值范围是[-7,13].
故答案为:[-7,13].
点评 本题给出二元一次不等式组,求目标函数z=x-2y的取值范围,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题.

练习册系列答案
相关题目
1.在△ABC中,点E满足$\overrightarrow{BE}=3\overrightarrow{EC}$,且$\overrightarrow{AE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m-n=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
2.为了普及法律知识,达到“法在心中”的目的,某市法制办组织了一次普法知识竞赛.统计局调查队从甲、乙两单位中各随机抽取了5名职工的成绩,如下:
(1)根据表中的数据,分别求出样本中甲、乙两单位职工成绩的平均数和方差,并判断哪个单位职工对法律知识的掌握更为稳定;
(2)用简单随机抽样的方法从乙单位的5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的成绩之差的绝对值至少是4分的概率.
| 甲单位职工的成绩(分) | 87 | 88 | 91 | 91 | 93 |
| 乙单位职工的成绩(分) | 85 | 89 | 91 | 92 | 93 |
(2)用简单随机抽样的方法从乙单位的5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的成绩之差的绝对值至少是4分的概率.
20.设F1、F2是双曲线C的两个焦点,若曲线C上存在一点P与F1关于曲线C的一条渐近线对称,则双曲线C的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |