题目内容
1．在△ABC中，点E满足$\overrightarrow{BE}=3\overrightarrow{EC}$，且$\overrightarrow{AE}=m\overrightarrow{AB}+n\overrightarrow{AC}$，则m-n=（ ）| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | $-\frac{1}{3}$ | D． | $\frac{1}{3}$ |
分析 根据向量的加减的几何意义即可求出答案
解答 解：∵点E满足$\overrightarrow{BE}=3\overrightarrow{EC}$，
∴$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{3}{4}$（$\overrightarrow{AC}$-$\overrightarrow{AB}$）=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$，
∴m=$\frac{1}{4}$，n=$\frac{3}{4}$，
∴m-n=-$\frac{1}{2}$，
故选：B
点评 本题考查了向量加减的几何意义，这里利用平面向量基本定理，进行转化计算，属于基础题
练习册系列答案
相关题目
9．设△ABC的面积为S1，它的外接圆面积为S2，若△ABC的三个内角大小满足A：B：C=3：4：5，则$\frac{{S}_{1}}{{S}_{2}}$的值为（ ）
| A． | $\frac{25}{12π}$ | B． | $\frac{25}{24π}$ | C． | $\frac{3+\sqrt{3}}{2π}$ | D． | $\frac{3+\sqrt{3}}{4π}$ |
6．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≥0}\\{ax，x＜0}\end{array}\right.$若方程f（-x）=f（x）有五个不同的根，则实数a的取值范围为（ ）
| A． | （-∞，-e） | B． | （-∞，-1） | C． | （1，+∞） | D． | （e，+∞） |
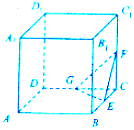如图所示，正方体ABCD-A1B1C1D1的棱长为1，E，F，G分别是棱BC，CC1，CD的中点，平面α过点B1且与平面EFG平行，则平面α被该正方体外接球所截得的截面圆的面积为为$\frac{2}{3}π$．