题目内容
18.已知正三棱柱的侧面展开图是相邻边长分别为3和6的矩形,则该正三棱柱的体积是$\frac{3\sqrt{3}}{2}或3\sqrt{3}$.分析 有边长分别为3和6,可以分两种情况来找三棱柱的底面积和高,再代入体积计算公式即可.
解答 解:因为正三棱柱的侧面展开图是边长分别为3和6的矩形,所以有以下两种情况,
①:3是下底面的周长,6是三棱柱的高,此时,下底面的边长为1,面积为:$\frac{\sqrt{3}}{4}$,
所以正三棱柱的体积为6×$\frac{\sqrt{3}}{4}$=$\frac{3\sqrt{3}}{2}$
②:6是下底面的周长,3是三棱柱的高,此时,下底面的边长为2,面积为$\sqrt{3}$,所以正三棱柱的体积为3$\sqrt{3}$,
故答案为:$\frac{3\sqrt{3}}{2}或3\sqrt{3}$.
点评 本题的易错点在于只求一种情况,应该注意考虑问题的全面性.分类讨论是高中数学的常考思想,在运用分类讨论思想做题时,要做到不重不漏.

练习册系列答案
相关题目
20.已知M(a,b)是圆O:x2+y2=r2内不在坐标轴上的一点,直线l的方程为ax+by=r2,直线m被圆O所截得的弦的中点为M,则下列说法中正确的是( )
| A. | m∥l且l与圆O相交 | B. | m⊥l且l与圆O相切 | C. | m∥l且l与圆O相离 | D. | m⊥l且l与圆O相离 |
7.已知二面角α-l-β为60°,如果平面角α内一点A到平面β的距离为$\sqrt{3}$,那么A到棱的距离为( )
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
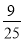 B.
B.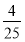 C.
C.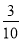 D.
D.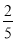
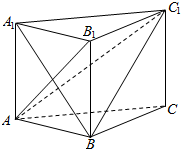 如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.
如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.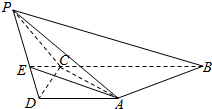 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.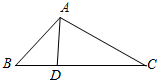
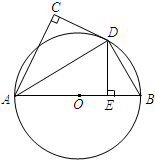 如图,AB为⊙O的直径,直线CD与⊙O相切于点D,AC⊥CD,DE⊥AB,C、E为垂足,连接AD,BD.若AC=4,DE=3,求BD的长.
如图,AB为⊙O的直径,直线CD与⊙O相切于点D,AC⊥CD,DE⊥AB,C、E为垂足,连接AD,BD.若AC=4,DE=3,求BD的长.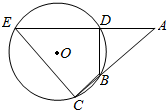 如图,⊙O的弦ED,CB的延长线交于点A.
如图,⊙O的弦ED,CB的延长线交于点A.