题目内容
已知f(x)=lnx,g(x)=
ax2+bx(a≠0),h(x)=f(x)-g(x)
(Ⅰ)若a=3,b=2,求h(x)的极大值点;
(Ⅱ)若b=2且h(x)存在单调递减区间,求a的取值范围.
| 1 |
| 2 |
(Ⅰ)若a=3,b=2,求h(x)的极大值点;
(Ⅱ)若b=2且h(x)存在单调递减区间,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)将a、b的值代入,可得h(x)=lnx-
x2-2x,求出其导数,再在区间(0,+∞)上讨论导数的正负,可以得出函数h(x)单调区间,进而得到h(x)的极大值点;
(Ⅱ)先求函数h(x)的解析式,因为函数h(x)存在单调递减区间,所以不等式h′(x)<0有解,通过讨论a的正负,得出h′(x)<0有解,即可得出a的取值范围.
| 3 |
| 2 |
(Ⅱ)先求函数h(x)的解析式,因为函数h(x)存在单调递减区间,所以不等式h′(x)<0有解,通过讨论a的正负,得出h′(x)<0有解,即可得出a的取值范围.
解答:
解:(Ⅰ)∵a=3,b=2,∴h(x)=f(x)-g(x)=lnx-
x2-2x,
∴h′(x)=
-3x-2=-
(x>0),
令h′(x)=0,则3x2+2x-1=0,x1=-1,x2=
,
则当0<x<
时,h′(x)>0,则h(x)在(0,
)上为增函数,
当x>
时,h′(x)<0,则h(x)在(
,+∞)上为减函数,
则h(x)的极大值点为
;
(Ⅱ)∵b=2,∴h(x)=lnx-
ax2-2x,
∴h′(x)=
-ax-2=-
,
∵函数h(x)存在单调递减区间,
∴h′(x)<0有解.
即当x>0时,则ax2+2x-1>0在(0,+∞)上有解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,y=ax2+2x-1>0在(0,+∞)总有解.
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而y=ax2+2x-1>0在(0,+∞)总有解,
则△=4+4a>0,且方程y=ax2+2x-1=0至少有一个正根,此时,-1<a<0
综上所述,a的取值范围为(-1,0)∪(0,+∞).
| 3 |
| 2 |
∴h′(x)=
| 1 |
| x |
| 3x2+2x-1 |
| x |
令h′(x)=0,则3x2+2x-1=0,x1=-1,x2=
| 1 |
| 3 |
则当0<x<
| 1 |
| 3 |
| 1 |
| 3 |
当x>
| 1 |
| 3 |
| 1 |
| 3 |
则h(x)的极大值点为
| 1 |
| 3 |
(Ⅱ)∵b=2,∴h(x)=lnx-
| 1 |
| 2 |
∴h′(x)=
| 1 |
| x |
| ax2+2x-1 |
| x |
∵函数h(x)存在单调递减区间,
∴h′(x)<0有解.
即当x>0时,则ax2+2x-1>0在(0,+∞)上有解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,y=ax2+2x-1>0在(0,+∞)总有解.
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而y=ax2+2x-1>0在(0,+∞)总有解,
则△=4+4a>0,且方程y=ax2+2x-1=0至少有一个正根,此时,-1<a<0
综上所述,a的取值范围为(-1,0)∪(0,+∞).
点评:本题考查了利用导数研究函数的单调性、导数的几何意义,函数与方程的讨论等,属于中档题.

练习册系列答案
相关题目

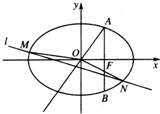 如图,已知椭圆C:
如图,已知椭圆C: