题目内容
17.若x,y满足约束条件$\left\{\begin{array}{l}2x+2y≥1\\ x≥y\\ 2x-y≤1\end{array}\right.$,则目标函数z=3x+2y的最大值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 作出可行域,变形目标函数,平移直线y=-$\frac{3}{2}$x可得结论.
解答  解:作出约束条件$\left\{\begin{array}{l}2x+2y≥1\\ x≥y\\ 2x-y≤1\end{array}\right.$所对应的可行域(如图△ABC),
解:作出约束条件$\left\{\begin{array}{l}2x+2y≥1\\ x≥y\\ 2x-y≤1\end{array}\right.$所对应的可行域(如图△ABC),
变形目标函数z=3x+2y可得y=-$\frac{3}{2}$x+$\frac{1}{2}$z,平移直线y=-$\frac{3}{2}$x可知,
当直线经过点A(1,1)时,直线的截距取最大值,z取最大值,
代值计算可得z的最大值为:5,
故选:C.
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
7.运行如图所示的程序框图,则输出的S值为( )
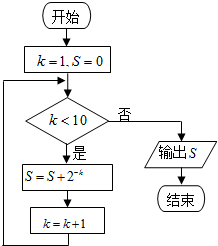

| A. | $\frac{{{2^9}-1}}{2^9}$ | B. | $\frac{{{2^9}+1}}{2^9}$ | C. | $\frac{{{2^{10}}-1}}{{{2^{10}}}}$ | D. | $\frac{{{2^{10}}}}{{{2^{10}}+1}}$ |
5.已知数列{an}满足an+1=2an,n∈N+,a3=4,则数列{an}的前5项和为( )
| A. | 32 | B. | 31 | C. | 64 | D. | 63 |
2.要得到函数y=sin$\frac{1}{2}$x的图象,只要将函数y=cos2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位长度,再将各点的横坐标伸长为原来的4倍,纵坐标不变 | |
| B. | 向左平移$\frac{π}{4}$个单位长度,再将各点的横坐标缩短为原来的$\frac{1}{4}$倍,纵坐标不变 | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再将各点的横坐标伸长为原来的4倍,纵坐标不变 | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再将各点的横坐标缩短到原来的$\frac{1}{4}$,纵坐标不变 |
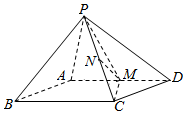 如图,四棱锥的底面ABCD是平行四边形,PA⊥平面ABCD,M是AD中点,N是PC中点.
如图,四棱锥的底面ABCD是平行四边形,PA⊥平面ABCD,M是AD中点,N是PC中点.