题目内容
1.若函数f(x)=$\frac{{2}^{x+1}}{{2}^{x}+1}$,则f(-$\frac{1}{3}$)+f(-$\frac{1}{2}$)+f(-1)+f(0)+f(1)+f($\frac{1}{2}$)+f($\frac{1}{3}$)=7.分析 先求出f(x)+f(-x)=2,由此能求出f(-$\frac{1}{3}$)+f(-$\frac{1}{2}$)+f(-1)+f(0)+f(1)+f($\frac{1}{2}$)+f($\frac{1}{3}$)的值.
解答 解:∵函数f(x)=$\frac{{2}^{x+1}}{{2}^{x}+1}$,
∴f(x)+f(-x)=$\frac{{2}^{x+1}}{{2}^{x}+1}$+$\frac{{2}^{-x+1}}{{2}^{-x}+1}$=$\frac{{2}^{x+1}}{{2}^{x}+1}$+$\frac{{2}^{\;}}{{2}^{x}+1}$=2,
∴f(-$\frac{1}{3}$)+f(-$\frac{1}{2}$)+f(-1)+f(0)+f(1)+f($\frac{1}{2}$)+f($\frac{1}{3}$)
=2×3+$\frac{2}{{2}^{0}+1}$=7.
故答案为:7.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设等比数列{an}的前n项和为Sn,若a3=4,S3=7,则S6的值为( )
| A. | 31 | B. | 32 | C. | 63 | D. | 64 |
9.若三条直线ax+y+1=0,y=3x,x+y=4,交于一点,则a的值为( )
| A. | 4 | B. | -4 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
16.由8个面围成的几何体,每个面都是正三角形,并且有四个顶点A,B,C,D在同一平面上,ABCD是边长为15的正方形,则该几何体的外接球的体积为( )
| A. | 1125$\sqrt{2}$π | B. | 3375$\sqrt{2}$π | C. | 450π | D. | 900π |
13.已知定义在R上的函数f(x)满足:y=f(x-1)的图象关于(1,0)点对称,且当x≥0时恒有$f(x-\frac{3}{2})=f(x+\frac{1}{2})$,当x∈[0,2)时,f(x)=ex-1,则f(2016)+f(-2017)=( )
| A. | -1-e | B. | e-1 | C. | 1-e | D. | e+1 |
10.已知函数f(x)=x3-6x2+9x,g(x)=$\frac{1}{3}$x3-$\frac{a+1}{2}$x2+ax-$\frac{1}{3}$(a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
| A. | (1,$\frac{9}{4}$] | B. | [9,+∞) | C. | (1,$\frac{9}{4}$]∪[9,+∞) | D. | [$\frac{3}{2}$,$\frac{9}{4}$]∪[9,+∞) |
11.已知焦点在y轴上的双曲线C的中心是原点O,离心率等于$\frac{{\sqrt{5}}}{2}$,以双曲线C的一个焦点为圆心,2为半径的圆与双曲线C的渐近线相切,则双曲线C的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{y^2}{4}-{x^2}=1$ | C. | ${y^2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ |
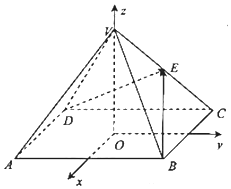 如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.
如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.