题目内容
13.已知定义在R上的函数f(x)满足:y=f(x-1)的图象关于(1,0)点对称,且当x≥0时恒有$f(x-\frac{3}{2})=f(x+\frac{1}{2})$,当x∈[0,2)时,f(x)=ex-1,则f(2016)+f(-2017)=( )| A. | -1-e | B. | e-1 | C. | 1-e | D. | e+1 |
分析 根据图象的平移可知y=f(x)的图象关于(0,0)点对称,可得函数为奇函数,由题意可知当x≥0时,函数为周期为2的周期函数,可得f(2016)+f(-2015)=f(0)-f(1),求解即可
解答 解:∵y=f(x-1)的图象关于(1,0)点对称,
∴y=f(x)的图象关于(0,0)点对称,
∴函数为奇函数,
∵当x≥0时恒有f(x+2)=f(x),当x∈[0,2)时,f(x)=ex-1,
∴f(2016)+f(-2017)
=f(2016)-f(2017)
=f(0)-f(1)
=0-(e-1)
=1-e,
故选:C.
点评 本题主要考查了函数图象的平移,奇函数的性质和函数的周期性.难点是对知识的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.过点M(0,1)和N(-1,m2)(m∈R)的直线的倾斜角α的取值范围是( )
| A. | 0°≤α<180° | B. | 45°≤α<180° | ||
| C. | 0°≤α≤45°或90°<α<180° | D. | 0°≤α≤45°或90°≤α<180° |
18.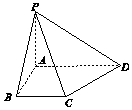 四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )
四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )
 四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )
四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )| A. | $\frac{\sqrt{42}}{7}$ | B. | $\frac{\sqrt{7}}{7}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
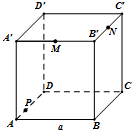 如图,在棱长为a的正方体ABCD-A′B′C′D′中,M、N分别是棱A′B′、B′C′的中点,P是棱AD上一点,AP=$\frac{a}{3}$,过P、M、N的平面与棱CD交于Q,则PQ的长度为$\frac{2\sqrt{\sqrt{2}}}{3}$a.
如图,在棱长为a的正方体ABCD-A′B′C′D′中,M、N分别是棱A′B′、B′C′的中点,P是棱AD上一点,AP=$\frac{a}{3}$,过P、M、N的平面与棱CD交于Q,则PQ的长度为$\frac{2\sqrt{\sqrt{2}}}{3}$a.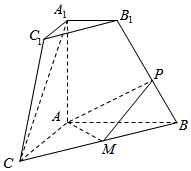 如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.
如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.