题目内容
5.已知f(x)=x2+2xf′(1),则f′(0)=-4.分析 把给出的函数求导得其导函数,在导函数解析式中取x=1可求2f′(1)的值.
解答 解:由f(x)=x2+2xf′(1),
得:f′(x)=2x+2f′(1),
取x=1得:f′(1)=2×1+2f′(1),
所以,f′(1)=-2.
故f′(0)=2f′(1)=-4,
故答案为:-4
点评 本题考查了导数运算,解答此题的关键是理解原函数解析式中的f′(1),在这里f′(1)只是一个常数,此题是基础题.

练习册系列答案
相关题目
13.函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( )
| A. | 在点x0处的斜率 | |
| B. | 在点(x0,f(x0))处的切线与x轴所夹的锐角的正切值 | |
| C. | 曲线y=f(x)在点(x0,f(x0))处切线的斜率 | |
| D. | 点(x0,f(x0))与点(0,0)连线的斜率 |
10.已知集合U=R,A={x|(x-2)(x+1)≤0},B={x|0≤x<3},则∁U(A∪B)=( )
| A. | (-1,3) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,-1)∪[3,+∞) |
17.已知△ABC中,满足b=2,B=60°的三角形有两解,则边长a的取值范围是( )
| A. | $\frac{\sqrt{3}}{2}$<a<2 | B. | $\frac{1}{2}$<a<2 | C. | 2<a<$\frac{4\sqrt{3}}{3}$ | D. | 2<a<2$\sqrt{3}$ |
15.设a=${log_{\frac{1}{3}}}$2,b=${log_{\frac{1}{2}}}\frac{1}{3}$,c=${(\frac{1}{2})^{0.3}}$,则( )
| A. | a<b<c | B. | b<a<c | C. | b<c<a | D. | a<c<b |
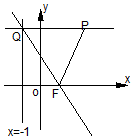 如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.
如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.