题目内容
已知关于 函数
函数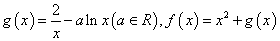 ,
,
(Ⅰ)试求函数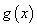 的单调区间;
的单调区间;
(Ⅱ)若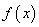 在区间
在区间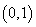 内有极值,试求a的取值范围;
内有极值,试求a的取值范围;
(Ⅲ)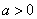 时,若
时,若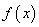 有唯一的零点
有唯一的零点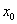 ,试求
,试求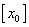 .
.
(注: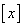 为取整函数,表示不超过
为取整函数,表示不超过 的最大整数,如
的最大整数,如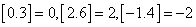 ;以下数据供参考:
;以下数据供参考: )
)
解:(Ⅰ)由题意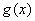 的定义域为
的定义域为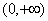
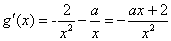
(i)若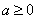 ,则
,则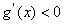 在
在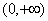 上恒成立,
上恒成立,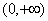 为其单调递减区间;
为其单调递减区间;
(ii)若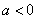 ,则由
,则由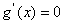 得
得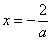 ,
,
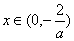 时,
时,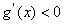 ,
,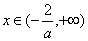 时,
时,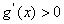 ,
,
所以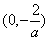 为其单调递减区间;
为其单调递减区间;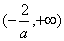 为其单调递增区间;
为其单调递增区间;
(Ⅱ)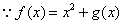
所以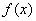 的定义域也为
的定义域也为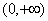 ,且
,且
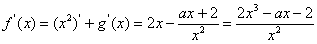
令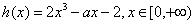 (*)
(*)
则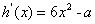 (**)
(**)
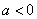 时,
时, 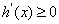 恒成立,所以
恒成立,所以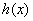 为
为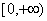 上的单调递增函数,又
上的单调递增函数,又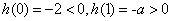 ,所以在区间
,所以在区间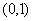 内
内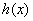 至少存在一个变号零点
至少存在一个变号零点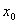 ,且
,且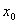 也是
也是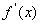 的变号零点,此时
的变号零点,此时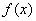 在区间
在区间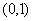 内有极值.
内有极值.
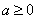 时
时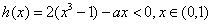 ,即在区间(0,1)上
,即在区间(0,1)上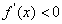 恒成立,此时,
恒成立,此时, 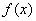 无极值.
无极值.
综上所述,若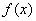 在区间
在区间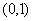 内有极值,则a的取值范围为
内有极值,则a的取值范围为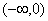 .
.
(Ⅲ)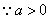 ,由(Ⅱ)且
,由(Ⅱ)且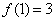 知
知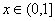 时
时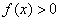 ,
, 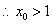 .
.
又由(*)及(**)式知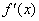 在区间
在区间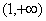 上只有一个极小值点,记为
上只有一个极小值点,记为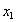 , 且
, 且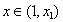 时
时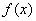 单调递减,
单调递减, 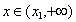 时
时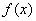 单调递增,由题意
单调递增,由题意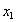 即为
即为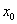 ,
,
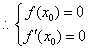
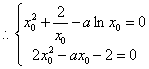
消去a,得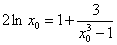
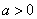 时令
时令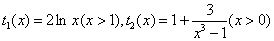 ,
,
则在区间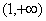 上为
上为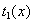 单调递增函数,
单调递增函数, 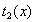 为单调递减函数,
为单调递减函数,
且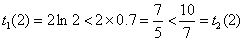
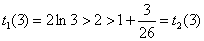
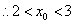

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 为
为 的函数,对任意
的函数,对任意 ,
, ,且
,且 ,
, ,则集合A中的最小元素是______.
,则集合A中的最小元素是______. 上的函数
上的函数 满足
满足 ,且
,且 时,
时, ,则
,则 。
。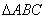 中,边a,b,c的对角分别为A,B,C;且
中,边a,b,c的对角分别为A,B,C;且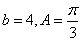 ,面积
,面积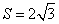 .
.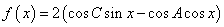 ,将
,将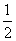 (纵坐标不变)得到
(纵坐标不变)得到 ,4) (B)(-
,4) (B)(- x
x [0,
[0, ],tanx
],tanx m”是真命题,则实数m的最小值为 .
m”是真命题,则实数m的最小值为 . 是奇函数,则使f(x)>3成立的x的取值范围为
是奇函数,则使f(x)>3成立的x的取值范围为 ) (B)(
) (B)( ) (C)(0,1) (D)(1,+
) (C)(0,1) (D)(1,+ )
)