题目内容
如图所示,在直角梯形PBCD中,PD∥BC,∠D=90°,PD=9,BC=3,CD=4,点A在PD上,且PA=2AD,将△PAB沿AB折到△SAB的位置,使SB⊥BC.
(Ⅰ)求证:SA⊥AD;
(Ⅱ)点E在SD上,且SE=
SD,求三棱锥E-ACD的体积.
(Ⅰ)求证:SA⊥AD;
(Ⅱ)点E在SD上,且SE=
| 1 |
| 3 |

考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:计算题,证明题,空间位置关系与距离
分析:(Ⅰ)由平面几何的知识,证得四边形ABCD为矩形,再由线面垂直的判定定理证得BC⊥平面SAB,从而证得
SA⊥AD;
(Ⅱ)在平面SAD内,过E作EH⊥AD,垂足为H,通过线面垂直的判定定理,证EH⊥平面ABD,并求出EH的长,再由三棱锥的体积公式即可得到结果.
SA⊥AD;
(Ⅱ)在平面SAD内,过E作EH⊥AD,垂足为H,通过线面垂直的判定定理,证EH⊥平面ABD,并求出EH的长,再由三棱锥的体积公式即可得到结果.
解答:
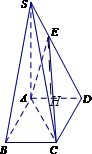
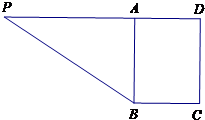 ( I)证明:∵PD=9,PA=2AD,
( I)证明:∵PD=9,PA=2AD,
∴PA=6,AD=3,
又∵BC=3,AD∥BC,∠D=90°,
∴四边形ABCD为矩形,AB⊥BC,
又∵SB⊥BC,AB∩SB=B,∴BC⊥平面SAB,
从而BC⊥SA,又∵BC∥AD,
∴SA⊥AD;
(Ⅱ)解:在平面SAD内,过E作EH⊥AD,垂足为H,
∵SA⊥AD,EH⊥AD,∴EH∥SA,
又∵SA⊥AB,∴EH⊥AB,而AB∩AD=A,∴EH⊥平面ABD,
即EH是三棱锥E-ACD底面ACD的高,
由EH∥SA,知
=
,又SE=
SD,∴
=
=
,
∴EH=
SA=4,
故VE-ACD=
×
AD•CD•EH=
×3×4×4=8.

 ( I)证明:∵PD=9,PA=2AD,
( I)证明:∵PD=9,PA=2AD,∴PA=6,AD=3,
又∵BC=3,AD∥BC,∠D=90°,
∴四边形ABCD为矩形,AB⊥BC,
又∵SB⊥BC,AB∩SB=B,∴BC⊥平面SAB,
从而BC⊥SA,又∵BC∥AD,
∴SA⊥AD;
(Ⅱ)解:在平面SAD内,过E作EH⊥AD,垂足为H,
∵SA⊥AD,EH⊥AD,∴EH∥SA,
又∵SA⊥AB,∴EH⊥AB,而AB∩AD=A,∴EH⊥平面ABD,
即EH是三棱锥E-ACD底面ACD的高,
由EH∥SA,知
| EH |
| SA |
| ED |
| SD |
| 1 |
| 3 |
| EH |
| SA |
| ED |
| SD |
| 2 |
| 3 |
∴EH=
| 2 |
| 3 |
故VE-ACD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查直线与平面的位置关系,考查线面垂直的判定和性质,同时考查棱锥的体积公式,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
设全集U={0,1,2,3,4,5,6,7,8,9},集合A={1,2,3,4,5},集合B={1,3,5,7,9},则∁UA∩∁UB为( )
| A、{6,8} |
| B、{0,6,8} |
| C、{1,3,5} |
| D、{1,2,3,4,5,7,9} |