题目内容
若函数f(x)=
(x>0),则f(
)+f(
)+f(2)+f(3)= .
| lnx |
| |lnx|+1 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:函数的值
专题:函数的性质及应用
分析:由已知得f(
)+f(
)+f(2)+f(3)=
+
+
+
=0.
| 1 |
| 3 |
| 1 |
| 2 |
| -ln3 |
| ln3+1 |
| -ln2 |
| ln2+1 |
| ln2 |
| ln2+1 |
| ln3 |
| ln3+1 |
解答:
解:∵函数f(x)=
(x>0),
∴f(
)+f(
)+f(2)+f(3)
=
+
+
+
=0.
故答案为:0.
| lnx |
| |lnx|+1 |
∴f(
| 1 |
| 3 |
| 1 |
| 2 |
=
| -ln3 |
| ln3+1 |
| -ln2 |
| ln2+1 |
| ln2 |
| ln2+1 |
| ln3 |
| ln3+1 |
=0.
故答案为:0.
点评:本题考查函数值的求法,是基础题,解题时要注意函数性质的合理运用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
用反证法证明命题:“已知a、b为实数,若a>0,b<0,则方程x2+ax+b=0?至少有一个实根”时,要做的假设是( )
| A、方程x2+ax+b=0没有实根 |
| B、方程x2+ax+b=0至多有一个实根 |
| C、方程x2+ax+b=0至多有两个实根 |
| D、方程x2+ax+b=0恰好有两个实根 |
已知点(1,-1)和(-2,1)在直线3x-2y-a=0的两侧,则a的取值范围是( )
| A、(-5,8) |
| B、(-8,5) |
| C、(-∞,-5)∪(8,+∞) |
| D、(-∞,-8)∪(5,+∞) |
已知集合A={x|x≥4},g(x)=
的定义域为B,若A∩B=∅,则实数a的取值范围是( )
| 1 | ||
|
| A、(-2,4) |
| B、(3,+∞) |
| C、(-∞,3) |
| D、(-∞,3] |
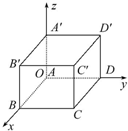 如图,已知长方体ABCD-A′B′C′D的边长为AB=12,AD=8,AA′=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA′分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,
如图,已知长方体ABCD-A′B′C′D的边长为AB=12,AD=8,AA′=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA′分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,