题目内容
13.在平面直角坐标系xOy中,过点M(1,0)的直线l与圆x2+y2=5交于A,B两点,其中A点在第一象限,且$\overrightarrow{BM}$=2$\overrightarrow{MA}$,则直线l的方程为x-y-1=0.分析 由题意,设直线x=my+1与圆x2+y2=5联立,利用韦达定理,结合向量知识,即可得出结论.
解答 解:由题意,设直线x=my+1与圆x2+y2=5联立,可得(m2+1)y2+2my-4=0,
设A(x1,y1),B(x2,y2),则y1=-2y2,y1+y2=-$\frac{2m}{{m}^{2}+1}$,y1y2=-$\frac{4}{{m}^{2}+1}$
联立解得m=1,∴直线l的方程为x-y-1=0,
故答案为:x-y-1=0.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设a,b为实数,若复数$\frac{1+3i}{a-bi}$=1-i(i为虚数单位),则( )
| A. | a=-1,b=-2 | B. | a=-1,b=2 | C. | a=1,b=2 | D. | a=1,b=-2 |
1.设a∈R,若复数z=$\frac{a-i}{3+i}$(i是虚数单位)的实部为2,则复数z的虚部为( )
| A. | 7 | B. | -7 | C. | 1 | D. | -1 |
18.设复数z满足$\frac{z}{|3+4i|}$=$\frac{1-i}{3-4i}$(其中i为虚数单位),则z的共轭复数为( )
| A. | $\frac{-7-i}{5}$ | B. | $\frac{-7+i}{5}$ | C. | $\frac{7+i}{5}$ | D. | $\frac{7-i}{5}$ |
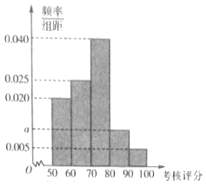 2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).
2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).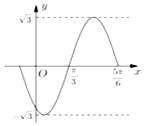 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )