题目内容
 如图,某渠道的截面是一个等腰梯形,上底 AD长为一腰和下底长之和,且两腰 A B,CD与上底 AD之和为8米,试问:等腰梯形的腰与上、下底长各为多少时,截面面积最大?并求出截面面积S的最大值.
如图,某渠道的截面是一个等腰梯形,上底 AD长为一腰和下底长之和,且两腰 A B,CD与上底 AD之和为8米,试问:等腰梯形的腰与上、下底长各为多少时,截面面积最大?并求出截面面积S的最大值.考点:函数最值的应用
专题:计算题,函数的性质及应用
分析:先表示梯形的面积,再利用配方法,即可得出结论.
解答:
解:设腰AB=CD=x米,则上底AD为8-2x,下底BC为8-3x,所以梯形的高为
x.
由x>0,8-2x>0,8-3x>0,可得0<x<
.…(4分)
∵S=
(8-3x+8-2x)•
x=
(-5x2+16x)═-
(x-
)2+
,…(7分)
∴x=
时,Smax=
(16×
-5×
)=
.
此时,上底AD=
米,下底BC=
米,最大截面面积最大为
平方米.…(10分)
| ||
| 2 |
由x>0,8-2x>0,8-3x>0,可得0<x<
| 8 |
| 3 |
∵S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
5
| ||
| 4 |
| 8 |
| 5 |
16
| ||
| 5 |
∴x=
| 8 |
| 5 |
| ||
| 4 |
| 8 |
| 5 |
| 64 |
| 25 |
16
| ||
| 5 |
此时,上底AD=
| 24 |
| 5 |
| 16 |
| 5 |
16
| ||
| 5 |
点评:本题考查利用数学知识解决实际问题,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
圆x2+y2+2x+4y-2=0上到直线x+y+1=0的距离为
的点个数为( )
| ||
| 2 |
| A、1 | B、2 | C、3 | D、4 |
“p或q为假”是“p且q为假”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
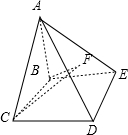 如图,在空间图形A-BCDE中,AB⊥平面BCDE,底面BCDE是直角梯形,且∠CBE=90°,BC∥DE,AB=DE=BE=
如图,在空间图形A-BCDE中,AB⊥平面BCDE,底面BCDE是直角梯形,且∠CBE=90°,BC∥DE,AB=DE=BE=