题目内容
4.已知函数f(x)=$(\frac{1}{2})^{|x+m-1|}$是偶函数,g(x)=$\left\{\begin{array}{l}{f(x)}&{x≥0}\\{{x}^{2}+2x+m}&{x<0}\end{array}\right.$,则方程g(x)=|x+$\frac{3}{4}$|实数根的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据f(x)是偶函数可得m=1,作出g(x)与y=|x+$\frac{3}{4}$|的函数图象,根据图象交点个数得出结论.
解答 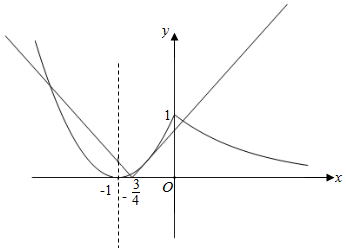 解:∵f(x)=($\frac{1}{2}$)|x+m-1|是偶函数,
解:∵f(x)=($\frac{1}{2}$)|x+m-1|是偶函数,
∴|x+m-1|=|-x+m-1|,
∴m=1.
∴g(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≥0}\\{{x}^{2}+2x+1,x<0}\end{array}\right.$,
作出y=g(x)与y=|x+$\frac{3}{4}$|的函数图象如图所示:
把y=x+$\frac{3}{4}$代入y=x2+2x+1得x2+x+$\frac{1}{4}$=0,
∵方程x2+x+$\frac{1}{4}$=0只有一解x=-$\frac{1}{2}$,∴直线y=|x+$\frac{3}{4}$|在(-$\frac{3}{4}$,0)上的函数图象与g(x)的图象相切,
由图象可知y=g(x)与y=|x+$\frac{3}{4}$|的函数图象有4个交点,
∴方程g(x)=|x+$\frac{3}{4}$|有4个实数根.
故选C.
点评 本题考查了偶函数的性质,方程的根与函数图象的关系,属于中档题.

练习册系列答案
相关题目
15.若双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线过点(2,$\sqrt{21}$),则此双曲线的离心率为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{13}}{2}$ |
19.已知向量$\overrightarrow{a}$=($\sqrt{3}$,1),$\overrightarrow{b}$=(sin2x,cos2x),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$,则函数f(x)的最小正周期为( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
16.已知复数z满足z=i(1-i),(i为虚数单位)则|z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
13.若X~B(n,$\frac{1}{3}$),且D(X)=$\frac{2}{3}$,则P(0≤X≤2)等于( )
| A. | $\frac{1}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{26}{27}$ | D. | $\frac{1}{27}$ |
10.已知双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{{b}^{2}}=1$(b>0),以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于A、B、C、D四点,四边形ABCD的面积为2b,则双曲线方程为( )
| A. | $\frac{{x}^{2}}{4}-\frac{3{y}^{2}}{4}=1$ | B. | $\frac{{x}^{2}}{4}-\frac{4{y}^{2}}{3}=1$ | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{8}=1$ | D. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$ |