题目内容
设x,y,z∈(0,1).求证x(1-y)+y(1-z)+z(1-x)<1.
考点:不等式的证明
专题:证明题,函数的性质及应用,不等式的解法及应用
分析:方法一、构造函数f(x)=1-[x(1-y)+y(1-z)+z(1-x)]=(y+z-1)x+(yz+1-y-z),再计算f(0),f(1),结合f(x)的图象,即可得证;
方法二、构造边长为1的正三角形ABC,在AB,BC,AC上分别取D,E,F,使得AD=x,BE=z,CF=y,再由S△ADF+S△BDE+S△CEF<S△ABC,运用面积公式计算即可得证.
方法二、构造边长为1的正三角形ABC,在AB,BC,AC上分别取D,E,F,使得AD=x,BE=z,CF=y,再由S△ADF+S△BDE+S△CEF<S△ABC,运用面积公式计算即可得证.
解答:
证法一:构造函数f(x)=1-[x(1-y)+y(1-z)+z(1-x)]
=(y+z-1)x+(yz+1-y-z),
∵0<y<1,0<z<1,
∴f(0)=yz+1-y-z=(1-y)(1-z)>0,
f(1)=y+z-1+(yz+1-y-z)=yz>0
由于函数f(x)的图象为一条直线,
则有当0<x<1,恒有f(x)>0成立,
故原不等式成立.
证法二:构造边长为1的正三角形ABC,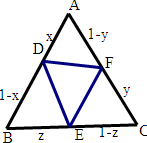
在AB,BC,AC上分别取D,E,F,使得AD=x,BE=z,CF=y,
则BD=1-x,CE=1-z,AF=1-y,
由于S△ADF+S△BDE+S△CEF<S△ABC,
即有
x(1-y)•sin60°+
z(1-x)•sin60°+
y(1-z)•sin60°<
×1×1×sin60°,
即有x(1-y)+z(1-x)+y(1-z)<1.
则原不等式成立.
=(y+z-1)x+(yz+1-y-z),
∵0<y<1,0<z<1,
∴f(0)=yz+1-y-z=(1-y)(1-z)>0,
f(1)=y+z-1+(yz+1-y-z)=yz>0
由于函数f(x)的图象为一条直线,
则有当0<x<1,恒有f(x)>0成立,
故原不等式成立.
证法二:构造边长为1的正三角形ABC,

在AB,BC,AC上分别取D,E,F,使得AD=x,BE=z,CF=y,
则BD=1-x,CE=1-z,AF=1-y,
由于S△ADF+S△BDE+S△CEF<S△ABC,
即有
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即有x(1-y)+z(1-x)+y(1-z)<1.
则原不等式成立.
点评:本题考查不等式的证明,考查构造法证明不等式的方法:构造函数和构造图形法,考查推理和运算能力,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知异面直线a,b均与平面α相交,下列命题:
(1)存在直线m?α,使得m⊥a或m⊥b.
(2)存在直线m?α,使得m⊥a且m⊥b.
(3)存在直线m?α,使得m与a和b所成的角相等.
其中不正确的命题个数为( )
(1)存在直线m?α,使得m⊥a或m⊥b.
(2)存在直线m?α,使得m⊥a且m⊥b.
(3)存在直线m?α,使得m与a和b所成的角相等.
其中不正确的命题个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知集合A={x||x-1|<2},集合B={x|lnx>0},则集合A∩B=( )
| A、(1,3) |
| B、(0,3) |
| C、(-1,3) |
| D、(-1,1) |
 如图,双曲线
如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、1+
| ||
B、4+2
| ||
C、2
| ||
D、2
|
如图,阴影部分的面积是( )
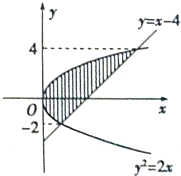

| A、16 | B、18 | C、20 | D、22 |