题目内容
若
,则cosα+sinα的取值范围是 .
|
考点:三角函数的最值,三角函数值的符号,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:首先,根据不等式的基本性质,得到cosα+sinα>0,然后,借助于辅助角公式确定其范围.
解答:
解:∵
,
∴
,
∴cosα+sinα>0,
∵cosα+sinα=
sin(α+
)≤
,
∴cosα+sinα∈(0,
].
故答案为:(0,
].
|
∴
|
∴cosα+sinα>0,
∵cosα+sinα=
| 2 |
| π |
| 4 |
| 2 |
∴cosα+sinα∈(0,
| 2 |
故答案为:(0,
| 2 |
点评:本题重点考查了辅助角公式、三角函数的图象与性质、不等式的基本性质等知识,属于中档题.命题角度比较新颖,需要注意此类题的解题方法.

练习册系列答案
相关题目
已知g(x)=1-2x,f[g(x)]=
,则f(-3)等于( )
| 1 |
| 2x+2 |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
若{1,2}⊆A⊆{1,2,3,4,5}}则满足条件的集合A的个数是( )
| A、6 | B、7 | C、8 | D、9 |
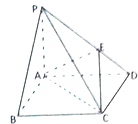 已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.
已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.