题目内容
20.若复数z满足$\frac{zi}{z-i}$=1,其中i为虚数单位,则复数z的模为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 利用复数的运算法则、模的计算公式即可得出.
解答 解:$\frac{zi}{z-i}$=1,∴zi=z-i,∴z=$\frac{i}{1-i}$=$\frac{i(1+i)}{(1-i)(1+i)}$=$-\frac{1}{2}$+$\frac{1}{2}$i,
则复数|z|=$\sqrt{(-\frac{1}{2})^{2}×2}$=$\frac{\sqrt{2}}{2}$.
故选:A.
点评 本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.若角α=-4,则α的终边在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
15.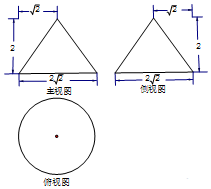 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )
 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )| A. | $\frac{1}{8}$ | B. | 1 | C. | 2 | D. | $\frac{4π}{3}$ |
10.直线l:y=k(x+$\sqrt{2}$)与曲线C:x2-y2=1(x<0)相交于P,Q两点,则直线l的倾斜角的取值范围是( )
| A. | ($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$) | B. | ($\frac{π}{4}$,$\frac{3π}{4}$) | C. | (0,$\frac{π}{2}$)∪($\frac{π}{2}$,π) | D. | [0,π) |
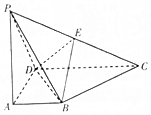 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.