题目内容
下列命题中错误的是( )
| A、命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0” | ||
| B、对命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 | ||
| C、已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假 | ||
D、若x、y∈R,则“x=y”是“xy≥(
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用逆否命题的定义即可判断出;
B.利用¬p的定义即可判断出;
C.若p∨q为假命题,则命题p与q都是假命题;
D.利用基本不等式的性质即可判断出等号成立的条件.
B.利用¬p的定义即可判断出;
C.若p∨q为假命题,则命题p与q都是假命题;
D.利用基本不等式的性质即可判断出等号成立的条件.
解答:
解:对于A.利用逆否命题的定义可知正确;
对于B.利用¬p的定义可知正确;
对于C.若p∨q为假命题,则命题p与q都是假命题,因此不正确;
对于D.x、y∈R,则“x=y”是“xy≥(
)2”成立的充要条件,正确.
故选:C.
对于B.利用¬p的定义可知正确;
对于C.若p∨q为假命题,则命题p与q都是假命题,因此不正确;
对于D.x、y∈R,则“x=y”是“xy≥(
| x+y |
| 2 |
故选:C.
点评:本题考查了简易逻辑的判定,属于基础题.

练习册系列答案
相关题目
设向量
,
,
满足
+
+
=
,且
•
=0,则|
|=3,|
|=4,则|
|=( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| a |
| c |
| b |
| A、5 | ||
B、
| ||
C、
| ||
| D、7 |
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),且当x>2时,f(x)单调递增,如果x1+x2<4,且(x1-2)(x2-2)<0,则下列说法正确的是( )
| A、f(x1)+f(x2)的值为正数 |
| B、f(x1)+f(x2)的值为负数 |
| C、f(x1)+f(x2)的值正负不能确定 |
| D、f(x1)+f(x2)的值一定为零 |
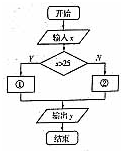 某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )
某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )| A、y=0.8xy=0.5x |
| B、y=0.5xy=0.8x |
| C、y=0.8x-7.5y=0.5x |
| D、y=0.8x+12.5y=0.8x |
某程序框图如图所示,执行该程序后输出的S的值是( )
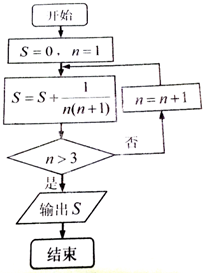

A、
| ||
B、
| ||
C、
| ||
D、
|
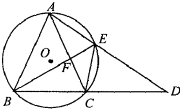 如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.