题目内容
5．若函数f（x）=$\frac{x}{（x+1）（x+a）}$的图象关于原点对称，则a=-1．分析 根据奇函数的图象的性质，可以函数f（x）图象关于原点对称，即f（x）为奇函数．
解答 解：∵函数f（x）=$\frac{x}{（x+1）（x+a）}$的图象关于原点对称，
∴函数f（x）为奇函数，
∴f（-x）=-f（x），
∴$\frac{-x}{（-x+1）（-x+a）}$=-$\frac{x}{（x+1）（x+a）}$，
∴（-x+1）（-x+a）=（x+1）（x+a）
解得，a=-1，
故答案为：-1．
点评 本题主要考查了奇函数的图象和性质，属于基础题．
练习册系列答案
相关题目
15．设全集U是实数集R，M={x∈Z|-2≤x≤2}，N={x∈N|-1＜x≤4}，则图中阴影部分所表示的集合是（ ）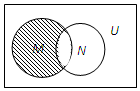 
| A． | {-2，-1} | B． | {0，1，2} | C． | {-2，-1，3} | D． | {-2，-1，0} |
13．原点到直线y=-$\frac{1}{2}$x+$\frac{5}{2}$的距离为（ ）
| A． | 1 | B． | $\sqrt{5}$ | C． | 2 | D． | $\sqrt{3}$ |
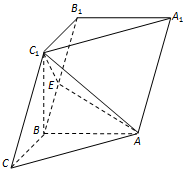如图在三棱柱ABC-A1B1C1中，已知AB⊥侧面BB1C1C，BC=BC1=$\sqrt{2}$，AB=CC1=2，点E在棱BB1上．