题目内容
已知函数f(x)=x2+
-1.
(1)判断函数f(x)在[2,4]上的单调性并证明;
(2)求函数f(x)在[2,4]上的最值.
| 16 |
| x |
(1)判断函数f(x)在[2,4]上的单调性并证明;
(2)求函数f(x)在[2,4]上的最值.
考点:函数单调性的性质,函数单调性的判断与证明,函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:(1)求导数,利用f′(x)=2x-
>0,即可得出函数f(x)在[2,4]上的单调性;
(2)利用单调性,即可求函数f(x)在[2,4]上的最值.
| 16 |
| x2 |
(2)利用单调性,即可求函数f(x)在[2,4]上的最值.
解答:
解:(1)∵f(x)=x2+
-1,
∴f′(x)=2x-
,
∵x∈[2,4],
∴f′(x)=2x-
>0,
∴函数f(x)在[2,4]上单调递增;
(2)由(1)知x=2时,函数f(x)的最小值为11,x=4时,函数f(x)的最大值为19.
| 16 |
| x |
∴f′(x)=2x-
| 16 |
| x2 |
∵x∈[2,4],
∴f′(x)=2x-
| 16 |
| x2 |
∴函数f(x)在[2,4]上单调递增;
(2)由(1)知x=2时,函数f(x)的最小值为11,x=4时,函数f(x)的最大值为19.
点评:本题考查函数单调性的判断与证明,考查函数的最值及其几何意义,比较基础.

练习册系列答案
相关题目
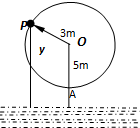 如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=
如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=