题目内容
已知集合A={x|
≥0}，B={x|x2-9x+14＜0}，C={x|5-a＜x＜a}．
（1）求A∪B，（∁RA）∩B；
（2）若C⊆（A∪B），求a的取值范围．
| 3-x |
| x-8 |
（1）求A∪B，（∁RA）∩B；
（2）若C⊆（A∪B），求a的取值范围．
考点：交、并、补集的混合运算,集合的包含关系判断及应用
专题：集合
分析：（1）先把集合A、B解出来，再求A∪B，（∁RA）∩B；
（2）由C⊆（A∪B），注意C=∅时也成立，再根据C是A∪B的子集解答即可．
（2）由C⊆（A∪B），注意C=∅时也成立，再根据C是A∪B的子集解答即可．
解答：
解：（1）解集合A={x|3≤x＜8}，B={x|2＜x＜7}，
∴A∪B={x|2＜x＜8}，
∁RA={x|x＜3或x≥8}，
∴（∁RA）∩B={x|2＜x＜3}；
（2）由（1）得A∪B={x|2＜x＜8}，
又C⊆（A∪B），
所以C=∅满足题意，即5-a≥a，解得a≤
，
或C⊆{x|2＜x＜8}，得：
，解得：
＜a≤3，
综上：a的取值范围是a≤3．
∴A∪B={x|2＜x＜8}，
∁RA={x|x＜3或x≥8}，
∴（∁RA）∩B={x|2＜x＜3}；
（2）由（1）得A∪B={x|2＜x＜8}，
又C⊆（A∪B），
所以C=∅满足题意，即5-a≥a，解得a≤
| 5 |
| 2 |
或C⊆{x|2＜x＜8}，得：
|
| 5 |
| 2 |
综上：a的取值范围是a≤3．
点评：本题主要考查集合的子交并补，属于基础题．
练习册系列答案
相关题目
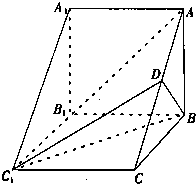如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，A1A=AB=2．