题目内容
10.下列命题中假命题的是( )| A. | ?x0∈R,lnx0<0 | B. | ?x∈(-∞,0),ex>x+1 | ||
| C. | ?x>0,5x>3x | D. | ?x0∈(0,+∞),x0<sinx0 |
分析 根据对数函数以及指数函数的性质分别判断各个选项即可.
解答 解:对于A:比如x0=$\frac{1}{e}$时,ln$\frac{1}{e}$=-1,是真命题;
对于B:令f(x)=ex-x-1,f′(x)=ex-1<0,f(x)递减,
∴f(x)>f(0)=0,是真命题;
对于C:函数y=ax(a>1)时是增函数,是真命题,
对于D:令g(x)=x-sinx,g′(x)=1-cosx≥0,g(x)递增,
∴g(x)>g(0)=0,是假命题;
故选:D.
点评 本题考查了命题的判断,考查函数的性质,是一道基础题.

练习册系列答案
相关题目
1.下列函数中,在定义域内是偶函数,且值域为[0,+∞)的是( )
| A. | f(x)=x2 | B. | f(x)=2x-1 | C. | f(x)=x2+cosx | D. | f(x)=xsinx |
18.设全集为实数集R,M={x|x∈R|x≤$\sqrt{5}$},N={1,2,3,4},则∁RM∩N=( )
| A. | {4} | B. | {3,4} | C. | {2,3,4} | D. | {1,2,3,4} |
15.若命题$p:?x∈(0,+∞),{log_2}(x+\frac{1}{x})≥1$,命题$q:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则下列命题为真命题的是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | (¬p)∧(¬q) |
2.设集合A={x|x≥-1},B={x|y=ln(x-2)},则A∩(∁RB)=( )
| A. | [-1,+∞) | B. | [-1,2] | C. | [2,+∞) | D. | [-1,2) |
19.下列说法不正确的是( )
| A. | 度与弧度是度量角的两种不同的度量单位 | |
| B. | 1度的角是圆周长的$\frac{1}{360}$所对的圆心角,1弧度的角是圆周的$\frac{1}{2π}$所对的圆心角 | |
| C. | 根据弧度的定义,知180°一定等于π弧度 | |
| D. | 不论是用角度制还是弧度制度量角,角的大小都与圆的半径长短有关 |
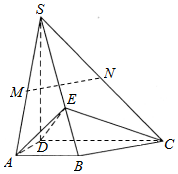 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.