题目内容
20.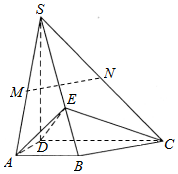 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.(1)证明:MN∥平面ABCD;
(2)证明:DE⊥平面SBC.
分析 (Ⅰ)连AC,则MN∥AC,由此能证明MN∥平面ABCD.
(Ⅱ)连结BD,推导出DB⊥BC,SD⊥BC,从而BC⊥平面SDB,BC⊥DE,由题意得△EBD∽△DBS,由此能证明DE⊥平面SBC.
解答  (本小题满分12分)
(本小题满分12分)
证明:(Ⅰ)连AC,∵M,N分别为SA,SC的中点,∴MN∥AC,
又∵MN?平面ABCD,AC?平面ABCD,
∴MN∥平面ABCD.(5分)
(Ⅱ)连结BD,∵BD2=12+12=2,BC2=12+(2-1)2=2,
BD2+BC2=2+2=4=DC2,∴DB⊥BC,
又SD⊥底面ABCD,BC?底面ABCD,∴SD⊥BC,
∵SD∩DB=D,∴BC⊥平面SDB,
∵DE?平面SDB,∴BC⊥DE,
又SB=$\sqrt{S{D}^{2}+D{B}^{2}}$=$\sqrt{4+2}$=$\sqrt{6}$,
当SE=2ED时,EB=$\frac{\sqrt{6}}{3}$,
在△EBD与△DBS中,$\frac{EB}{BD}$=$\frac{\frac{\sqrt{6}}{3}}{\sqrt{2}}$=$\frac{\sqrt{3}}{3}$,$\frac{DB}{BS}$=$\frac{\sqrt{2}}{\sqrt{6}}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{EB}{BD}$=$\frac{DB}{BS}$,
又∠EBD=∠DBS,∴△EBD∽△DBS,
∴∠DEB=∠SDB=90°,即DE⊥SB.
∵SB∩BC=B,
∴DE⊥平面SBC.(12分)
点评 本题考查线面平行的证明,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
3.若圆C:x2+y2-4x+4y+m=与x轴交于A、B两点,且∠ACB=120°,则实数m的值为( )
| A. | 24 | B. | -8 | C. | 8 | D. | 4 |
8.设实数p在[0,5]上随机地取值,使方程x2+px+1=0有实根的概率为( )
| A. | 0.6 | B. | 0.5 | C. | 0.4 | D. | 0.3 |
5.在等差数列{an}中,a4=2,且a1+a2+…+a10=65,则公差d的值是( )
| A. | 4 | B. | 3 | C. | 1 | D. | 2 |
12.在区间[0,π]上随机地取一个数x,则事件“sinx≤$\frac{1}{2}$”发生的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
10.下列命题中假命题的是( )
| A. | ?x0∈R,lnx0<0 | B. | ?x∈(-∞,0),ex>x+1 | ||
| C. | ?x>0,5x>3x | D. | ?x0∈(0,+∞),x0<sinx0 |