题目内容
直线y=x+1按向量
=(-1,k)平移后与圆(x-1)2+(y+2)2=2相切,则实数k的值为 .
| a |
考点:圆的切线方程
专题:直线与圆
分析:直线y=x+1按向量
=(-1,k)平移后,得到的直线方程为x-y+2+k=0,由题圆心(1,-2)到直线x-y+2+k=0的距离等于圆的半径
,由此能求出实数k的值.
| a |
| 2 |
解答:
解:直线y=x+1按向量
=(-1,k)平移后,
得到的直线方程为y-k=x+2,即x-y+2+k=0,
∵直线y=x+1按向量
=(-1,k)平移后与圆(x-1)2+(y+2)2=2相切,
∴圆心(1,-2)到直线x-y+2+k=0的距离:
d=
=
,
解得k=-3或k=-7.
故答案为:-3或-7.
| a |
得到的直线方程为y-k=x+2,即x-y+2+k=0,
∵直线y=x+1按向量
| a |
∴圆心(1,-2)到直线x-y+2+k=0的距离:
d=
| |1+2+2+k| | ||
|
| 2 |
解得k=-3或k=-7.
故答案为:-3或-7.
点评:本题考查实数k的值的求法,是基础题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
相关题目
将周期为π的函数y=sin2ωx+2sinωxcosωx-cos2ωx(ω>0)的图象按
=(-
,1)平移后,所得函数图象的解析式为( )
| a |
| π |
| 8 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=1-
|
函数y=
在区间[3,6]上的最小值是( )
| 4 |
| x-2 |
| A、1 | B、3 | C、-2 | D、5 |
函数f(x)=Asin(ωx+ϕ)+k在一个周期内的图象如图,函数f(x)解析式为( )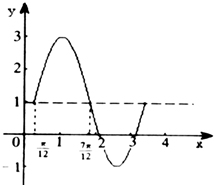

A、f(x)=4sin(
| ||||
B、f(x)=2sin(2x-
| ||||
C、f(x)=4sin(
| ||||
D、f(x)=2sin(2x-
|
已知x,y均为正数,且x≠y,则下列四个数中最小的一个是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
己知关于x的方程(m+3)x2-4mx+2m-1=0 的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是( )
| A、-3<m<0 |
| B、0<m<3 |
| C、m<-3或m>0 |
| D、m<0 或 m>3 |
已知集合M={y|y=x2-1(x∈R)},P={x|y=
,x∈R},则M∩P=( )
| 3-x2 |
A、{(-
| ||||
B、{t|1≤t≤
| ||||
C、{t|-1≤t≤
| ||||
D、{t|0≤t≤
|