题目内容
 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.(Ⅰ)求这50名学生百米测试成绩的平均数
. |
| x |
(Ⅱ)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1的概率.
考点:频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图先估算出这50名学生百米测试成绩的平均数
,进而根据方差公式,计算出答案.
(2)由频率分布直方图得到成绩在[13,14)和[17,18]内的频率,然后用50分别乘以两组的频率可得第一、五组中的学生数,分别设出两组中的学生的成绩,然后用枚举法写出从第一、五组中随机取出两个成绩的总的取法种数N,找出取出的两个成绩的差的绝对值大于1的取法种数n,则从第一、五组中随机取出两个成绩,这两个成绩的差的绝对值大于1的概率P=
.
. |
| x |
(2)由频率分布直方图得到成绩在[13,14)和[17,18]内的频率,然后用50分别乘以两组的频率可得第一、五组中的学生数,分别设出两组中的学生的成绩,然后用枚举法写出从第一、五组中随机取出两个成绩的总的取法种数N,找出取出的两个成绩的差的绝对值大于1的取法种数n,则从第一、五组中随机取出两个成绩,这两个成绩的差的绝对值大于1的概率P=
| n |
| N |
解答:
解:(1)由频率分布直方图知,成绩在[13,14)的人数为50×0.06×1=3(人),
成绩在[14,15)的人数为50×0.16×1=8(人),
成绩在[15,16)的人数为50×0.38×1=19(人),
成绩在[16,17)的人数为50×0.32×1=16(人),
成绩在[17,18]的人数为50×0.08×1=4(人),
故这50名学生百米测试成绩的平均数
=
(13.5×3+14.5×8+15.5×19+16.5×16+17.5×4)=15.7;
方差s2=
[(13.5-15.7)2×3+(14.5-15.7)2×8+(15.5-15.7)2×19+(16.5-15.7)2×16+(17.5-15.7)2×4]=1
(2)并设第一组三人的成绩分别为x、y、z;
第五组四人的成绩分别为A、B、C、D;
则从第一、五组中随机取出两个成绩的总的取法种数为:
xy,xz,yz,AB,AC,AD,BC,BD,CD,xA,xB,xC,xD,yA,yB,yC,yD,zA,zB,zC,zD共21(种).
取出的两个成绩的差的绝对值大于1的取法种数为:
xA,xB,xC,xD,yA,yB,yC,yD,zA,zB,zC,zD共12(种).
则从第一、五组中随机取出两个成绩,这两个成绩的差的绝对值大于1的概率为P=
=
.
成绩在[14,15)的人数为50×0.16×1=8(人),
成绩在[15,16)的人数为50×0.38×1=19(人),
成绩在[16,17)的人数为50×0.32×1=16(人),
成绩在[17,18]的人数为50×0.08×1=4(人),
故这50名学生百米测试成绩的平均数
. |
| x |
| 1 |
| 50 |
方差s2=
| 1 |
| 50 |
(2)并设第一组三人的成绩分别为x、y、z;
第五组四人的成绩分别为A、B、C、D;
则从第一、五组中随机取出两个成绩的总的取法种数为:
xy,xz,yz,AB,AC,AD,BC,BD,CD,xA,xB,xC,xD,yA,yB,yC,yD,zA,zB,zC,zD共21(种).
取出的两个成绩的差的绝对值大于1的取法种数为:
xA,xB,xC,xD,yA,yB,yC,yD,zA,zB,zC,zD共12(种).
则从第一、五组中随机取出两个成绩,这两个成绩的差的绝对值大于1的概率为P=
| 12 |
| 21 |
| 4 |
| 7 |
点评:本题考查了频率分布直方图,考查了古典概型及其概率计算公式,解答此题的两个关键点是:一、明确频率分布直方图中纵轴的单位;二、古典概型及其概率的计算.解答(2)时除了枚举法之外,也可运用排列组合知识求解.此题属中低档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若∅?{x|x2≤a,a∈R},则实数a的取值范围是( )
| A、(0,+∞) |
| B、[0,+∞) |
| C、(-∞,0] |
| D、(-∞,0) |
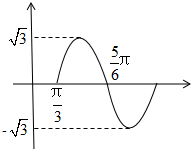 已知函数y=Asin(ωx+φ)(A>0,ω>0),一个周期内的函数图象,如图所示,求:
已知函数y=Asin(ωx+φ)(A>0,ω>0),一个周期内的函数图象,如图所示,求: