题目内容
下列命题中：
①
•（
-
）=
•
-
•
；
②
•（
•
）=（
•
）•
；
③（
-
）2=|
|2-2|
|•|
|+|
|2；
④若
•
=0，则
=0或
=0；
⑤若
•
=
•
，则
=
；
⑥|
|2=
2；
⑦
=
；
⑧（
•
）2=
2•
2；
⑨（
-
）2=
2-2
•
+
2．
其中正确的是 ．
①
| a |
| b |
| c |
| a |
| b |
| a |
| c |
②
| a |
| b |
| c |
| a |
| b |
| c |
③（
| a |
| b |
| a |
| a |
| b |
| b |
④若
| a |
| b |
| a |
| b |
⑤若
| a |
| b |
| c |
| b |
| a |
| c |
⑥|
| a |
| a |
⑦
| ||||
|
| ||
|
⑧（
| a |
| b |
| a |
| b |
⑨（
| a |
| b |
| a |
| a |
| b |
| b |
其中正确的是
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据平面向量数量积的定义与运算性质，对每一个命题进行分析与判定，即可得出正确的结论．
解答：
解：对于①，根据平面向量数量积的运算律，得分配律成立，∴命题正确；
对于②，根据平面向量数量积的运算律，得结合律不成立，∴命题错误；
对于③，（
-
）2=|
|2-2|
|•|
|cos＜
，
＞+|
|2，∴命题错误；
对于④，当
•
=0时，
=
，或
=
，或
⊥
，∴命题错误；
对于⑤，当
•
=
•
时，（
-
）•
=0，∴
-
=
，或
=
，或（
-
）⊥
，∴命题错误；
对于⑥，|
|2=|
|×|
|=|
|×|
|×cos0°=
2，∴命题正确；
对于⑦，
=
=
≠
，∴命题错误；
对于⑧，（
•
）2=|
|2×|
|2×cos2＜
，
＞≠|
|2×|
|2=
2•
2，∴命题错误；
对于⑨，（
-
）2=（
-
）•（
-
）=
2-2
•
+
2，∴命题正确．
综上，正确的命题是①⑥⑨．
故答案为：①⑥⑨．
对于②，根据平面向量数量积的运算律，得结合律不成立，∴命题错误；
对于③，（
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
对于④，当
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
对于⑤，当
| a |
| b |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
| 0 |
| b |
| 0 |
| a |
| c |
| b |
对于⑥，|
| a |
| a |
| a |
| a |
| a |
| a |
对于⑦，
| ||||
|
|
| ||||||||
|
|
|
| ||||||
|
|
| ||
|
对于⑧，（
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
对于⑨，（
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
综上，正确的命题是①⑥⑨．
故答案为：①⑥⑨．
点评：本题通过命题真假的判定，综合考查了平面向量数量积的定义与运算性质的应用问题，是基础知识的综合应用问题．
练习册系列答案
相关题目
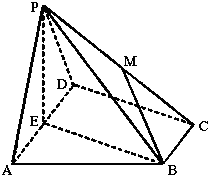如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD的中点，M是棱PC的中点，PA=PD=2，BC=