题目内容
18.下列结论正确的是( )| A. | 当x>0且x≠1时,$lgx+\frac{1}{lgx}≥2$ | B. | 当x>0时,$\sqrt{x}+\frac{1}{{\sqrt{x}}}≥2$ | ||
| C. | 当x≥2时,$x+\frac{1}{x}≥2$ | D. | 当0<x≤2时,$x-\frac{1}{x}$无最大值 |
分析 A.x∈(0,1)时,lgx<0,不成立.
B.利用基本不等式的性质即可得出成立.
C.x≥2时,f(x)=x+$\frac{1}{x}$,利用导数研究其单调性即可得出.
D.0<x≤2时,y=f(x)=$x-\frac{1}{x}$,利用导数研究其单调性即可得出.
解答 解:A.x∈(0,1)时,lgx<0,不成立.
B.利用基本不等式的性质即可得出成立.
C.x≥2时,f(x)=x+$\frac{1}{x}$,f′(x)=1-$\frac{1}{{x}^{2}}$>0,函数f(x)单调递增,∴f(x)$≥2+\frac{1}{2}$=$\frac{5}{2}$,因此不成立.
D.0<x≤2时,y=f(x)=$x-\frac{1}{x}$,y′=1+$\frac{1}{{x}^{2}}$>0,∴函数f(x)单调递增,∴f(x)≤f(2),因此D不成立.
故选:B.
点评 本题考查了基本不等式的性质、利用导数研究其单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.函数f(x)=2x-8的零点是( )
| A. | 3 | B. | (3,0) | C. | 4 | D. | (4,0) |
9.执行如图所示的程序框图,则输出的k的值是( )
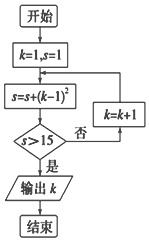

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1.若实数x,y满足约束条件$\left\{\begin{array}{l}y≤4-x\\ 2x-y+1≥0\\ x-4y-4≤0\end{array}\right.$,则z=x-2y的最大值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.若函数f(x)是奇函数,且在(0,+∞)上是增函数,又f(-3)=0,则(x-2)f(x)<0的解集是( )
| A. | (-3,0)∪(2,3) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(2,+∞) |
6.下列四组中的f(x),g(x),表示同一个函数的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | ||
| C. | f (x)=x2,g(x)=($\sqrt{x}$)4 | D. | f(x)=|x|,g(x)=$\sqrt{x^2}$ |
 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.