题目内容
20．若点P（-1，$\sqrt{3}$）在圆x2+y2=m上，点Q（x0，y0）在圆x2+y2=m内，则d=$\sqrt{{x}_{0}^{2}+{y}_{0}^{2}}$的取值范围为[0，2）．分析 由点在圆上可得m值，由点在圆内可得x02+y02的范围，开方可得．
解答 解：∵点P（-1，$\sqrt{3}$）在圆x2+y2=m上，
∴1+3=m，解得m=4，
∵点Q（x0，y0）在圆x2+y2=4内，
∴x02+y02＜4，∴d=$\sqrt{{x}_{0}^{2}+{y}_{0}^{2}}$＜2，
故d=$\sqrt{{x}_{0}^{2}+{y}_{0}^{2}}$的取值范围为[0，2）
故答案为：[0，2）
点评 本题考查点与圆的位置关系，属基础题．
练习册系列答案
相关题目
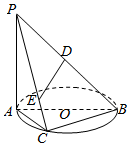如图，AB是圆O的直径，点C是半圆的中点，PA⊥平面ABC，PA=AB，PB=6D是PB的中点，E是PC上一点．