题目内容
11.已知$\overrightarrow{a}$、$\overrightarrow{b}$为互相垂直的单位向量,若向量$\overrightarrow{c}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1,则|$\overrightarrow{c}$|的取值范围是[$\sqrt{2}$-1,$\sqrt{2}$+1].分析 作出图形,由平面向量线性运算的几何意义可知C在以P为圆心,以1为半径的圆上.其中P为$\overrightarrow{a}+\overrightarrow{b}$的终点.
解答 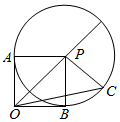 解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,$\overrightarrow{OP}=\overrightarrow{a}+\overrightarrow{b}$,则|OA|=|OB|=1,OA⊥OB,
解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,$\overrightarrow{OP}=\overrightarrow{a}+\overrightarrow{b}$,则|OA|=|OB|=1,OA⊥OB,
∴|OP|=$\sqrt{2}$,
∵|$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$|=1,即|$\overrightarrow{OP}-\overrightarrow{OC}$|=|$\overrightarrow{CP}$|=1,
∴C在以P为圆心,以1为半径的圆上,
∴$\sqrt{2}-1$≤|OC|≤$\sqrt{2}+1$.
故答案为:[$\sqrt{2}-1$,$\sqrt{2}+1$].
点评 本题考查了平面向量线性运算的几何意义,属于基础题.

练习册系列答案
相关题目
1.已知圆C:x2+y2=1,点P(x0,y0)在直线l:3x+2y-4=0上,若在圆C上总存在两个不同的点A、B,使$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OP}$,则x0的取值范围是 ( )
| A. | (0,$\frac{24}{13}$) | B. | (-$\frac{24}{13}$,0) | C. | (0,$\frac{13}{24}$) | D. | (0,$\frac{13}{12}$) |
19.为了得到函数$y=sin(2x+\frac{π}{3})$的图象,可将函数y=sin2x的图象向左平移m个单位长度或向右平移n个单位长度(m,n均为正数),则|m-n|的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
6.设$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(m,1),如果向量$\overrightarrow{a}$+$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$平行,则$\overrightarrow{a}$•$\overrightarrow{b}$等于( )
| A. | -$\frac{5}{2}$ | B. | -2 | C. | -1 | D. | 0 |
16.直线x=0的倾斜角为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | 1 | D. | 以上都不对 |