题目内容
20.设常数θ∈(0,$\frac{π}{2}$),函数f(x)=2cos2(θ-$\frac{3}{2}$x)-1,且对任意实数x,f(x)=f($\frac{π}{3}$-x)恒成立.(1)求θ值;
(2)试把f(x)表示成关于sinx的关系式;
(3)若x∈(0,π)时,不等式f(x)>2a•f($\frac{2x}{3}$)-13f($\frac{x}{3}$)恒成立,求实数a的范围.
分析 (1)利用倍角公式降幂,结合f(x)=f($\frac{π}{3}$-x)恒成立求得cos2θ=0,从而求得θ值;
(2)把θ值代入即可求得f(x)关于sinx的关系式;
(3)把f(x)>2a•f($\frac{2x}{3}$)-13f($\frac{x}{3}$)转化为cos2x-acosx+3>0.令cosx=t(-1<t<1),则t2-at+3>0在t∈(-1,1)上恒成立,再转化为关于a的不等式组求解.
解答 解:(1)f(x)=2cos2(θ-$\frac{3}{2}$x)-1=cos(2θ-3x),
则f($\frac{π}{3}-x$)=cos(2θ-π+3x)=-cos(2θ+3x).
由f(x)=f($\frac{π}{3}$-x),得cos(2θ-3x)=-cos(2θ+3x),
即cos(2θ-3x)+cos(2θ+3x)=0,
∴2cos2θcos3x=0,则cos2θ=0,
∵θ∈(0,$\frac{π}{2}$),∴θ=$\frac{π}{4}$;
(2)f(x)=2cos2(θ-$\frac{3}{2}$x)-1=cos(2θ-3x)=cos($\frac{π}{2}-3x$)=sin3x=3sinx-4sin3x;
(3)由f(x)>2a•f($\frac{2x}{3}$)-13f($\frac{x}{3}$),得sin3x>2asin2x-13sinx,
∴3sinx-4sin3x>4asinxcosx-13sinx,即cos2x-acosx+3>0.
令cosx=t(-1<t<1),则t2-at+3>0在t∈(-1,1)上恒成立.
∴△=a2-12<0或$\left\{\begin{array}{l}{{a}^{2}-12≥0}\\{\frac{a}{2}≤-1}\\{a+4≥0}\end{array}\right.$或$\left\{\begin{array}{l}{{a}^{2}-12≥0}\\{\frac{a}{2}≥1}\\{4-a≥0}\end{array}\right.$.
解得:-4≤a≤4.
点评 本题考查恒成立问题,考查三角函数的性质的应用,训练了恒成立问题的求解方法,考查利用“三个二次”结合求解字母的取值范围,属中档题.

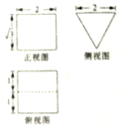
| A. | 20π | B. | $\frac{44}{3}$π | C. | $\frac{28}{3}$π | D. | 4π |
| A. | f(x)在$(0,\frac{π}{2})$单调递减 | B. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递减 | ||
| C. | f(x)在$(0,\frac{π}{2})$单调递增 | D. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递增 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 60° | B. | 30° | C. | 90° | D. | 45° |
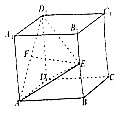 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.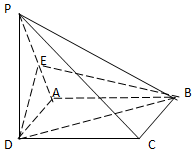 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: