题目内容
1.若y=f(x)是幂函数,且满足f(4)=2f(2),则f(3)=3.分析 设出幂函数y=f(x)的解析式,根据题意求出α的值,得出f(x)的解析式,再计算f(3).
解答 解:设幂函数y=f(x)=xα,α∈R,
由f(4)=2f(2),
得4α=2•2α,
∴22α=2α+1,
即2α=α+1,
解得α=1,
∴f(x)=x,
∴f(3)=3.
故答案为:3.
点评 本题考查了幂函数的定义与应用问题,是基础题目.

练习册系列答案
相关题目
11.设函数$f(x)=sin(ωx+φ)-\sqrt{3}cos(ωx+φ)$($ω>0,|φ|<\frac{π}{2}$)的最小正周期为π,且f(x)为奇函数,则( )
| A. | f(x)在$(0,\frac{π}{2})$单调递减 | B. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递减 | ||
| C. | f(x)在$(0,\frac{π}{2})$单调递增 | D. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递增 |
6.已知m,n∈R,则“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.下列命题中正确的是( )
| A. | 空间任三点可以确定一个平面 | |
| B. | 垂直于同一条直线的两条直线必互相平行 | |
| C. | 空间不平行的两条直线必相交 | |
| D. | 既不相交也不平行的两条直线是异面直线 |
10.在正方体ABCD-A1B1C1D1中,异面直线A1B与CC1所成角的大小为( )
| A. | 60° | B. | 30° | C. | 90° | D. | 45° |
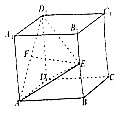 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.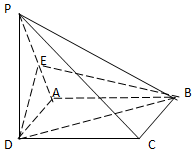 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: