题目内容
若x、y满足
，目标函数z=x-ky的最大值为9，则实数k的值是（ ）
|
| A、2 | B、-2 | C、1 | D、-1 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用数形结合确定目标函数的最优解，利用基本不等式即可得到结论．
解答：
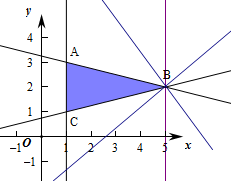解：作出不等式组对应的平面区域如图：
则A（1，3），B（5，2），C（1，1），
若k=0，则z=x，此时在B处函数取得最大值z=5，不满足条件．
若k＞0，则目标函数等价为y=
x+
，此时直线斜率为
＞0，
由图象可知当直线经过点B（5，2），直线截距最小，此时z最大为x-ky=9，
即5-2k=9，则2k=-4，解得k=-2，不满足条件．
若k＜0，则目标函数等价为y=
x+
，此时直线斜率为
＜0，
由图象可知当直线经过点B（5，2），直线截距最小，此时z最大为x-ky=9，
即5-2k=9，则2k=-4，解得k=-2，满足条件．
故选：B．
解：作出不等式组对应的平面区域如图：则A（1，3），B（5，2），C（1，1），
若k=0，则z=x，此时在B处函数取得最大值z=5，不满足条件．
若k＞0，则目标函数等价为y=
| 1 |
| k |
| z |
| -k |
| 1 |
| k |
由图象可知当直线经过点B（5，2），直线截距最小，此时z最大为x-ky=9，
即5-2k=9，则2k=-4，解得k=-2，不满足条件．
若k＜0，则目标函数等价为y=
| 1 |
| k |
| z |
| -k |
| 1 |
| k |
由图象可知当直线经过点B（5，2），直线截距最小，此时z最大为x-ky=9，
即5-2k=9，则2k=-4，解得k=-2，满足条件．
故选：B．
点评：本题主要考查线性规划和基本不等式的应用，利用数形结合是解决本题的关键，综合性较强．
练习册系列答案
小学教材完全解读系列答案
相关题目
i是虚数单位，则复数1-7i的模为（ ）
| A、50 | ||
| B、5 | ||
| C、8 | ||
D、5
|
命题“存在x0∈R，2x0≤0”的否定是（ ）
| A、不存在x0∈R，2x0＞0 |
| B、对任意的x∈R，2x≤0 |
| C、对任意的x∈R，2x＞0 |
| D、存在x0∈R，2x0≥0 |
已知
=
，则tanθ的值为（ ）
| 1+sinθ-cosθ |
| 1+sinθ+cosθ |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知n∈N，则方程C2n+2n=C2n+24-n的解为（ ）
| A、2 | B、1 | C、2或1 | D、2或3 |
下列各式中，能作为数列2，0，2，0…通项公式的一个是（ ）
| A、an=（-1）n+1 | ||
| B、an=（-1）n+1+1 | ||
C、an=
| ||
D、an=
|
设m，n分别是先后抛掷一枚骰子所得到的点数，则在先后两次出现的点数中有5的情况下，方程x2+mx+n=0有实根的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线ax+y+a-1=0不经过第一象限，则与该直线垂直的直线的倾斜角的取值范围（ ）
A、[
| ||||
B、（
| ||||
C、[0，
| ||||
D、（0，
|