题目内容
已知f(x)=ln(x+1) , g(x)=
ax2+bx (a,b∈R).
(1)若b=2且h(x)=f(x-1)-g(x)存在单调递减区间,求实数a的取值范围;
(2)若a=0,b=1,求证:当x∈(-1,+∞)时,f(x)-g(x)≤0恒成立;
(3)设x>0,y>0,证明:xlnx+ylny>(x+y)ln
.
| 1 |
| 2 |
(1)若b=2且h(x)=f(x-1)-g(x)存在单调递减区间,求实数a的取值范围;
(2)若a=0,b=1,求证:当x∈(-1,+∞)时,f(x)-g(x)≤0恒成立;
(3)设x>0,y>0,证明:xlnx+ylny>(x+y)ln
| x+y |
| 2 |
考点:利用导数研究函数的单调性,函数恒成立问题,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:本题第(1)题利用函数单调递减,导函数值为负(非正)解题;第(2)题是恒成立问题,转化为最大值问题去解;第(3)题构造函数,利用单调性得到相关结论,通过化简变形得到结果.
解答:
解:(1)当b=2时,h(x)=lnx-
ax2-2x
∴h′(x)=
-ax-2.
∵h(x)有单调减区间,
∴h'(x)<0有解,即
<0
∵x>0,∴ax2+2x-1>0有解.
(ⅰ)当a≥0时符合题意;
(ⅱ)当a<0时,△=4+4a>0,即a>-1.
∴a的取值范围是(-1,+∞).
(2)当a=0,b=1时,设φ(x)=f(x)-g(x)=ln(x+1)-x,
∴φ′(x)=
-1=
.
∵x>-1,
讨论φ'(x)的正负得下表:
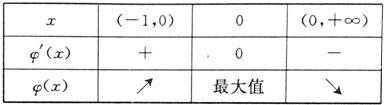
∴当x=0时φ(x)有最大值0.
即φ(x)≤0恒成立.
∴当x∈(-1,+∞)时,f(x)-g(x)≤0恒成立.
(3)∵x>0,y>0,
∴xlnx+ylny-(x+y)ln
=x(lnx-ln
)+y(lny-ln
)
=xln
+yln
=-xln
-yln
=-xln(1+
)-yln(1+
)
由(2)有-xln(1+
)-yln(1+
)>-x•
-y•
=0
∴xlnx+ylny>(x+y)ln
| 1 |
| 2 |
∴h′(x)=
| 1 |
| x |
∵h(x)有单调减区间,
∴h'(x)<0有解,即
| 1-ax2-2x |
| x |
∵x>0,∴ax2+2x-1>0有解.
(ⅰ)当a≥0时符合题意;
(ⅱ)当a<0时,△=4+4a>0,即a>-1.
∴a的取值范围是(-1,+∞).
(2)当a=0,b=1时,设φ(x)=f(x)-g(x)=ln(x+1)-x,
∴φ′(x)=
| 1 |
| x+1 |
| -x |
| x+1 |
∵x>-1,
讨论φ'(x)的正负得下表:

∴当x=0时φ(x)有最大值0.
即φ(x)≤0恒成立.
∴当x∈(-1,+∞)时,f(x)-g(x)≤0恒成立.
(3)∵x>0,y>0,
∴xlnx+ylny-(x+y)ln
| x+y |
| 2 |
| x+y |
| 2 |
| x+y |
| 2 |
=xln
| 2x |
| x+y |
| 2y |
| x+y |
| x+y |
| 2x |
| x+y |
| 2y |
| y-x |
| 2x |
| x-y |
| 2y |
由(2)有-xln(1+
| y-x |
| 2x |
| x-y |
| 2y |
| y-x |
| 2x |
| x-y |
| 2y |
∴xlnx+ylny>(x+y)ln
| x+y |
| 2 |
点评:本题(1)、(2)要求学生对导数与单调区间、最值的关系相当熟悉,第(3)题除了要求学生熟悉函数单调性的应用之外,还要能熟练运用对数运算进行变形,才能得到本题结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
双曲线y2-
=1的离心率e=2,则以双曲线的两条渐近线与抛物线y2=mx的交点为顶点的三角形的面积为( )
| x2 |
| m |
A、
| ||
B、9
| ||
C、27
| ||
D、36
|
 在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.
在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.