题目内容
14.下列说法中,正确的是( )| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 若随机变量X~N(3,1)则P(X<4)=p,则(2<X<4)=1-2p | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |
分析 A,众数是4和5;
B,随机变量X~N(3,1),则正太分布曲线关于x=3对称,当P(X<4)=p时,则(2<X<4)=2p-1;
C,数据2,3,4,5分别是数据4,6,8,10的2倍,根据公式D(ax+b)=a2DX,可判定;
D,频率分布直方图中各小长方形的面积等于相应各组的频率.
解答 解:对于A,众数是4和5,故错;
对于B,随机变量X~N(3,1),则正态分布曲线关于x=3对称,当P(X<4)=p时,则(2<X<4)=2p-1,故错;
对于C,∵数据2,3,4,5分别是数据4,6,8,10的2倍,根据公式D(ax+b)=a2DX,可判定该命题正确;
对于D,频率分布直方图中各小长方形的面积等于相应各组的频率,故错;
故选:C
点评 本题考查了命题真假的判定,涉及到了统计的知识,属于基础题.

练习册系列答案
相关题目
2.已知全集A={x|x≤9,x∈N*}集合B={x|0<x<7},则A∩B=( )
| A. | {x|0<x<7} | B. | {x|1≤x≤6} | C. | {1,2,3,4,5,6} | D. | {7,8,9} |
9.一个正三棱柱的正视图如图所示,已知它的体积为3,则该正三棱柱的高为( )
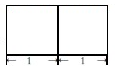

| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
6.角A是△ABC的一个内角,若命题p:A<$\frac{π}{3}$,命题q:sinA<$\frac{\sqrt{3}}{2}$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.设圆O1和圆O2是两个定圆,动圆P与这两个定圆都相切,则圆P的圆心轨迹可能是( )


| A. | ①③⑤ | B. | ②④⑤ | C. | ①②④ | D. | ①②③ |
4.公元前3世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(d)的立方成正比”,此即V=kd3,与此类似,我们可以得到:
(1)正四面体(所有棱长都相等的四面体)的体积(V)与它的棱长(a)的立方成正比,即V=ma3;
(2)正方体的体积(V)与它的棱长(a)的立方成正比,即V=na3;
(3)正八面体(所有棱长都相等的八面体)的体积(V)与它的棱长(a)的立方成正比,即V=ta3;
那么m:n:t=( )
(1)正四面体(所有棱长都相等的四面体)的体积(V)与它的棱长(a)的立方成正比,即V=ma3;
(2)正方体的体积(V)与它的棱长(a)的立方成正比,即V=na3;
(3)正八面体(所有棱长都相等的八面体)的体积(V)与它的棱长(a)的立方成正比,即V=ta3;
那么m:n:t=( )
| A. | 1:6$\sqrt{2}$:4 | B. | $\sqrt{2}$:12:16 | C. | $\frac{\sqrt{2}}{12}$:1:$\sqrt{2}$ | D. | $\sqrt{2}$:6:4$\sqrt{2}$ |
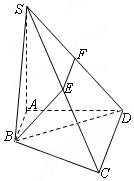 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.