题目内容
已知函数f(x)=log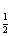
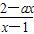 (a是常数且a<2).
(a是常数且a<2).
(1)求f(x)的定义域;
(2)若f(x)在区间(2,4)上是增函数,求a的取值范围.
(1)∵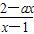 >0,∴(ax-2)(x-1)<0,
>0,∴(ax-2)(x-1)<0,
①当a<0时,函数的定义域为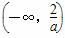 ∪(1,+∞);
∪(1,+∞);
②当a=0时,函数的定义域为(1,+∞);
③当0<a<2时,函数的定义域为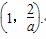 .
.
(2)∵f(x)在(2,4)上是增函数,
∴只要使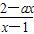 在(2,4)上是减函数且恒为正即可.
在(2,4)上是减函数且恒为正即可.
令g(x)=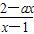 ,
,
即当x∈(2,4)时g′(x)≤0恒成立且g(4)≥0.
解法一:g′(x)=
∴当a-2<0,即a<2时,g′(x)≤0.
g(4)≥0,即1-2a≥0,∴a≤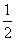 ,∴a∈
,∴a∈
解法二:∵g(x)=
∴要使g(x)=-a+ 在(2,4)上是减函数,只需2-a>0,∴a<2,
在(2,4)上是减函数,只需2-a>0,∴a<2,
以下步骤同解法一.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
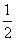 D.-2
D.-2