题目内容
已知f(x)为偶函数且满足关系f(2+x)=f(2-x),当-2≤x≤0时,f(x)=2x.若n∈N+,an=f(n),则a2 015等于( )
A.2 013 B.2
C.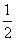 D.-2
D.-2
C
[解析] 设2+x=t,则∴x=t-2.
∴f(t)=f[2-(t-2)]
=f(4-t)=f(t-4).
∴f(x)的周期为4.
∴a2 015=f(2 015)=f(4×504-1)=f(-1)=2-1=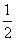 .
.

练习册系列答案
相关题目
 等于( )
等于( )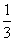 B.
B. C.
C. D.
D.
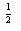 ,y=(x-1)2,y=x3中有3个是增函数;②若logm3<logn3<0,则0<n<m<1;③若函数f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;④已知函数f(x)=
,y=(x-1)2,y=x3中有3个是增函数;②若logm3<logn3<0,则0<n<m<1;③若函数f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;④已知函数f(x)=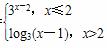 ,则方程f(x)=
,则方程f(x)=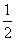 有2个实数根,其中正确命题的个数为( )
有2个实数根,其中正确命题的个数为( )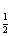
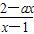 (a是常数且a<2).
(a是常数且a<2). -3x)+1,则f(lg2)+f(lg
-3x)+1,则f(lg2)+f(lg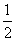 )=( )
)=( )