题目内容
已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定此二次函数.
解法1:利用二次函数一般式.
设f(x)=ax2+bx+c(a≠0).
由题意得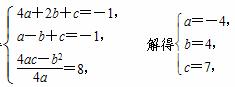
∴所求二次函数为f(x)=-4x2+4x+7.
解法2:利用二次函数的顶点式.
设f(x)=a(x-m)2+n(a≠0).
∵f(2)=f(-1),
∴抛物线对称轴为x=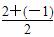 =
=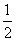 ,∴m=
,∴m=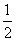 .
.
又根据题意函数有最大值y=8,∴y=f(x)=a 2+8.
2+8.
∵f(2)=-1,∴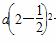 +8=-1,解得a=-4.
+8=-1,解得a=-4.
∴f(x)=-4 2+8=-4x2+4x+7.
2+8=-4x2+4x+7.
解法3:利用二次函数的两根式.
由已知f(x)+1=0的两根为x1=2,x2=-1,
故可设f(x)+1=a(x-2)(x+1)(a≠0),
即f(x)=ax2-ax-2a-1.
又函数有最大值ymax=8,即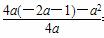 =8,
=8,
解得a=-4或a=0(舍去).
∴所求函数解析式为f(x)=-4x2+4x+7.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (x2-3x)的单调递减区间为________.
(x2-3x)的单调递减区间为________. 的是( )
的是( )
 等于( )
等于( )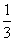 B.
B. C.
C. D.
D.
 则函数f(x)=1⊕2x的图象是( )
则函数f(x)=1⊕2x的图象是( )

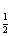
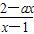 (a是常数且a<2).
(a是常数且a<2).