题目内容
已知锐角△ABC的三个内角A、B、C对边分别是 a、b、c，
=
．
（1）求证：角A、C、B成等差数列；
（2）若角A是△的最大内角，求cos（B+C）+
sinA的范围
（3）若△ABC的面积S△ABC=
，求△ABC 周长的最小值．
| a+b |
| cosA+cosB |
| c |
| cosC |
（1）求证：角A、C、B成等差数列；
（2）若角A是△的最大内角，求cos（B+C）+
| 3 |
（3）若△ABC的面积S△ABC=
| 3 |
考点：正弦定理,基本不等式
专题：综合题,解三角形
分析：（1）用正弦定理化边为角，化简得sin（A-C）=sin（C-B），利用正弦函数的单调性可得A-C=C-B；
（2）cos（B+C）+
sinA可化简为2sin(A-
)，由题意得
≤A＜
，
≤A-
＜
，据此可得结果；
（3）易求C=
，利用面积公式可得ab=4，c2=a2+b2-2abcosC=a2+b2-ab，利用基本不等式即可求得a+b+c的最小值；
（2）cos（B+C）+
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
（3）易求C=
| π |
| 3 |
解答：
解：（1）根据题意，在△ABC中，
由正弦定理得
=
，即sinAcosC+sinBcosC=sinCcosA+sinCcosB，
∴sin（A-C）=sin（C-B），
又A、B、C∈(0，
)，∴-
＜A-C＜
、-
＜C-B＜
，
而y=sinx在(-
，
)内单调递增，
∴A-C=C-B，即2C=A+B，角A、C、B成等差数列．
（2）在△ABC中，B+C=π-A，
∴cos(B+C)+
sinA=
sinA-cosA=2sin(A-
)，
由题意得
≤A＜
，
≤A-
＜
，
∴sin（A-
）∈[
，
)；
（3）由A+B+C=π及2C=A+B，得C=
，
∴S△ABC=
absinC=
⇒ab=4，
又c2=a2+b2-2abcosC=a2+b2-ab，
∴a+b+c=a+b+
≥2
+
=3
=6，
当且仅当a=b时，取等号，
∴△ABC的周长的最小值是6．
由正弦定理得
| sinA+sinB |
| cosA+cosB |
| sinC |
| cosC |
∴sin（A-C）=sin（C-B），
又A、B、C∈(0，
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
而y=sinx在(-
| π |
| 2 |
| π |
| 2 |
∴A-C=C-B，即2C=A+B，角A、C、B成等差数列．
（2）在△ABC中，B+C=π-A，
∴cos(B+C)+
| 3 |
| 3 |
| π |
| 6 |
由题意得
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴sin（A-
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
（3）由A+B+C=π及2C=A+B，得C=
| π |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
又c2=a2+b2-2abcosC=a2+b2-ab，
∴a+b+c=a+b+
| a2+b2-ab |
| ab |
| 2ab-ab |
| ab |
当且仅当a=b时，取等号，
∴△ABC的周长的最小值是6．
点评：该题考查正弦定理、余弦定理及其应用，考查利用基本不等式求函数最值，考查学生综合运用知识分析解决问题的能力．
练习册系列答案
相关题目
a表示函数y=sinx（-π≤x≤π）与x轴围成的图形的面积，则复数z=
（其中i为虚数单位）在复平面内对应的点位于（ ）
| (-1+i)(a+i) |
| -i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知向量
=（3，4），
=（-1，5），向量k
+2
与向量
=（2，-3）垂直，则k的值是（ ）
| a |
| b |
| a |
| b |
| c |
| A、2 | ||
B、-
| ||
| C、1 | ||
| D、-3 |
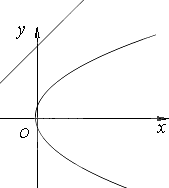已知点P是射线y=2（x＞1）上一点．过P作直线MN，交抛物线y2=4x于M，N两点，使点P平分线段MN．