题目内容
16.某几何体的三视图如图所示,则该几何体的体积为( )
| A. | $\frac{64π}{3}+2\sqrt{3}$ | B. | $\frac{56π}{3}+4\sqrt{3}$ | C. | 18π | D. | 22π+4 |
分析 已知中的三视图,可得:该几何体是一个圆柱切去两个弓形柱所得的几何体,进而可得答案.
解答 解:已知中的三视图,可得:该几何体是一个圆柱切去两个弓形柱所得的几何体,
圆柱的底面半径为2,高为6,
故体积为:6×π•22=24π,
弓形弦到圆心的距离为2-1=1,
故弓形弦所对的圆心角为:$\frac{2π}{3}$,
故弓形的面积为:$\frac{4π}{3}-\sqrt{3}$,
弓形柱的高为2,
故两个弓形柱的体积为:4×($\frac{4π}{3}-\sqrt{3}$),
故组合体的体积为:24π-4×($\frac{4π}{3}-\sqrt{3}$)=$\frac{56π}{3}+4\sqrt{3}$,
故选:B
点评 本题考查的知识点是棱柱的体积和表面积,圆柱的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
6.执行如图所示的程序框图,则输出的结果为( )
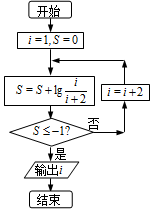

| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
4.函数f(x)=2x-sinx的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
1.双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$右焦点到渐近线的距离为( )
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{12}{5}$ |
18.已知集合 A={-2,-1,0,2,3},B={y|y=|x|,x∈A},则A∩B=( )
| A. | {0,1,2,3} | B. | {2,3} | C. | {0,1,2} | D. | {0,2,3} |
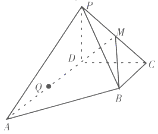 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4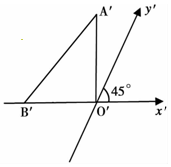 如图所示,△A′O′B′表示水平放置△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=8,则△AOB的边OB上的高为16$\sqrt{2}$.
如图所示,△A′O′B′表示水平放置△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=8,则△AOB的边OB上的高为16$\sqrt{2}$.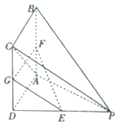 如图,四棱锥P-ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD