题目内容
5．
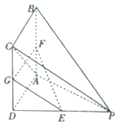如图，四棱锥P-ABCD的底面ABCD是正方形，分E，F，G别为PD，AB，CD的中点，PD⊥平面ABCD（1）证明AC⊥PB
（2）证明：平面PBC∥平面EFG．
分析 （1）连结BD，推导出PD⊥AC，BD⊥AC，从而AC⊥平面PBD，由此能证明AC⊥PB．
（2）推导出GE∥平面PBC，GF∥平面PBC，由此能证明平面PBC∥平面EFG．
解答 证明：（1）连结BD，
∵PD⊥平面ABCD，∴PD⊥AC，
∵底面ABCD是正方形，∴BD⊥AC，
又PD∩BD=D，∴AC⊥平面PBD，
∵PB?平面PBD，∴AC⊥PB．
（2）∵G、E分别为CD、PD的中点，∴CE∥PC，
又GE?平面PBC，PC?平面PBC，
∴GE∥平面PBC，
在正方形ABCD中，G、F分别为CD、AB的中点，
∴GF∥BC，又GF?平面PBC，BC?平面PBC，
∴GF∥平面PBC，
∵GF∩GE=G，∴平面PBC∥平面EFG．
点评 本题考查线线垂直的证明，考查面面平行的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
16．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $\frac{64π}{3}+2\sqrt{3}$ | B． | $\frac{56π}{3}+4\sqrt{3}$ | C． | 18π | D． | 22π+4 |
13．点P（1，4）关于直线y=-x的对称点的坐标是（ ）
| A． | （1，-4） | B． | （-4，1） | C． | （4，-1） | D． | （-4，-1） |
10．已知x，y满足$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y≤1}\end{array}\right.$，z=2x+y的最大值为m，若正数a，b满足a+b=m，则$\frac{1}{a}+\frac{4}{b}$的最小值为（ ）
| A． | 9 | B． | $\frac{3}{2}$ | C． | $\frac{4}{3}$ | D． | $\frac{5}{2}$ |
17．已知sin（α+$\frac{π}{3}$）=sinα，则tanα=（ ）
| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |
6．已知集合M={x|lg（x-2）≤0}，P={y|-1≤y≤3}，则M∩P=（ ）
| A． | ∅ | B． | {x|2＜x＜3} | C． | M | D． | {x|x≤3} |
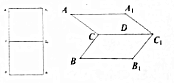已知：矩形AA1B1B，且AB=2AA1=2，C1，C分别是A1B1、AB的中点，D为C1C中点，将矩形AA1B1B沿着直线C1C折成一个60°的二面角，如图所示．