题目内容
1.求下列函数的导数.(1)y=$\frac{\sqrt{{x}^{5}}+\sqrt{{x}^{7}}+\sqrt{{x}^{9}}}{\sqrt{x}}$
(2)f(x)=2-2sin2$\frac{x}{2}$.
分析 先化简f(x),再求导.
解答 解:(1)y=x2+x3+x4,y′=2x+3x2+4x3;
(2)y=1+cosx,y′=-sinx.
点评 本题考查了基本初等函数的导数,属于基础题,先化简f(x)是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.不等式$\frac{2-x}{1+x}$≥0的解集为( )
| A. | (-1,2] | B. | [-1,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪(2,+∞) |
16.设函数f(x)=x3-ax2+2bx+1的导函数为f′(x),若函数f′(x)的图象关于直线x=$\frac{2}{3}$对称,且当x∈[1,π]时,恒有f(x)≥1,则实数b的取值范围为( )
| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,1] | C. | (-∞,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,+∞) |
11.在空间直角坐标系中,在x轴上的点P(m,0,0)到点P1(4,1,2)的距离为$\sqrt{30}$,则m的值为( )
| A. | -9或1 | B. | 9或-1 | C. | 5或-5 | D. | 2或3 |
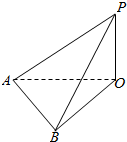 如图所示,在地面上有一旗杆OP,测得它的高度10m,在地面上取一基线AB,AB=20m,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,则∠AOB=$\frac{π}{2}$.
如图所示,在地面上有一旗杆OP,测得它的高度10m,在地面上取一基线AB,AB=20m,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,则∠AOB=$\frac{π}{2}$.