在四边形ABCD中.若$\overrightarrow{DC}=\frac{2}{5}\overrightarrow{AB}$.且|$\overrightarrow{AD}|=|\overrightarrow{BC}|$.则这个四边形是( )A．平行四边形B．菱形C．矩形D．等腰梯形题目和参考答案——青夏教育精英家教网—

题目内容

7．在四边形ABCD中，若$\overrightarrow{DC}=\frac{2}{5}\overrightarrow{AB}$，且|$\overrightarrow{AD}|=|\overrightarrow{BC}|$，则这个四边形是（　　）

A．

平行四边形

B．

菱形

C．

矩形

D．

等腰梯形

分析利用向量的共线、等腰梯形的定义即可判断出结论．

解答解：∵$\overrightarrow{DC}=\frac{2}{5}\overrightarrow{AB}$，且|$\overrightarrow{AD}$|=$|\overrightarrow{BC}|$，
∴DC∥AB，DC≠AB，AD=BC．
则这个四边形是等腰梯形．
故选：D．

点评本题考查了向量的共线、等腰梯形的定义，考查了推理能力与计算能力，属于基础题．

练习册系列答案

18．在△ABC中，$|{\overrightarrow{AB}+\overrightarrow{AC}}|=\sqrt{3}|{\overrightarrow{AB}-\overrightarrow{AC}}|$，$|{\overrightarrow{AB}}|=|{\overrightarrow{AC}}|=3$，则$\overrightarrow{CB}•\overrightarrow{CA}$的值为（　　）

15．

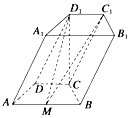如图，在四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD是等腰梯形，∠ADC=120°，AB=2CD=2，平面D₁DCC₁垂直平面ABCD，D₁C⊥AB，M是线段AB的中点．
（Ⅰ）求证：D₁M∥面B₁BCC₁；
（Ⅱ）若DD₁=2，求平面C₁D₁M和平面ABCD所成的锐角的余弦值．

2．设数列{a_n}是等差数列，数列{b_n}的前n项和S_n满足S_n=2（b_n-1），且a₂=b₁-1，a₅=b₃-1．
（Ⅰ）求数列{a_n}和{b_n}的通项公式；
（Ⅱ）设c_n=a_n•b_n，求数列{c_n}的前n项和T_n．

12．已知数列{$\frac{{a}_{n}}{2n-1}$}的前n项和为S_n，若S_n+$\frac{{4}^{n+1}}{{5}^{n}}$=4．
（1）求数列{a_n}的通项公式；
（2）求数列{a_n}的前n项和T_n．

19．函数f（x）=ax³+3x²+2，若f′（-1）=6，则a的值等于4．

16．过点P（1，1）且倾斜角为45°的直线被圆（x-2）²+（y-1）²=2所截的弦长是（　　）

17．关于x，y的不等式组$\left\{\begin{array}{l}{2x-y+1＞0}\\{x+m＜0}\\{y-m＞0}\end{array}\right.$，表示的平面区域为D，若存在点P（x₀，y₀）∈D，满足x₀-2y₀=2，则实数m的取值范围是m＜-$\frac{2}{3}$．

试题分类