题目内容
20.求下列各函数的定义域:(1)y=2tan$\frac{x}{2}$
(2)y=tan(x-$\frac{π}{3}$)
分析 直接由正切函数的定义域结合复合函数的定义域的求法求解两个函数的定义域.
解答 解:(1)由$\frac{x}{2}≠\frac{π}{2}+kπ$,得x≠π+2kπ,k∈Z,
∴y=2tan$\frac{x}{2}$的定义域为{x|x≠π+2kπ,k∈Z};
(2)由x-$\frac{π}{3}≠\frac{π}{2}+kπ$,得$x≠\frac{5π}{6}+kπ,k∈Z$,
∴y=tan(x-$\frac{π}{3}$)的定义域为{x|$x≠\frac{5π}{6}+kπ,k∈Z$}.
点评 本题考查与正切函数有关的复合函数的定义域的求法,是基础题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
10.已知方程(x2-mx+4)(x2-nx+4)=0的四个根组成一个首项$\frac{1}{4}$的等比数列,则|m-n|的值为( )
| A. | 0 | B. | $11\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
5.已知2sinα=2M+1有意义,则M的取值范围是( )
| A. | -$\frac{3}{2}$≤M≤$\frac{1}{2}$ | B. | M<-$\frac{3}{2}$ | C. | M>$\frac{1}{2}$ | D. | -3≤M≤1 |
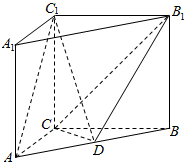 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.